Hierarchical clustering (계층적 군집화)

이전 포스팅: K-means clustering

이전 포스팅에서는 Hard, Partitional 특징을 갖는 K-means clustering을 정리했습니다.
이번 포스팅에서는 Hierarchical clustering을 정리해보고자 합니다.

Hierarchicl clustering은 거리가 가까운 데이터들을 그룹으로 묶어 주는 방법으로 계층적으로 진행된다 해서 붙은 이름입니다. 주로 뇌 데이터의 연결성 (Connectivity) 분석이나 유전체 데이터 분석에 많이 사용되는 방법입니다.

K-means와의 가장 큰 차이점은 partitional/hierarchical 특성이 있을 수 있으며, 군집의 개수 (k)의 사전 설정 유무입니다.

---

Hierarchical clustering

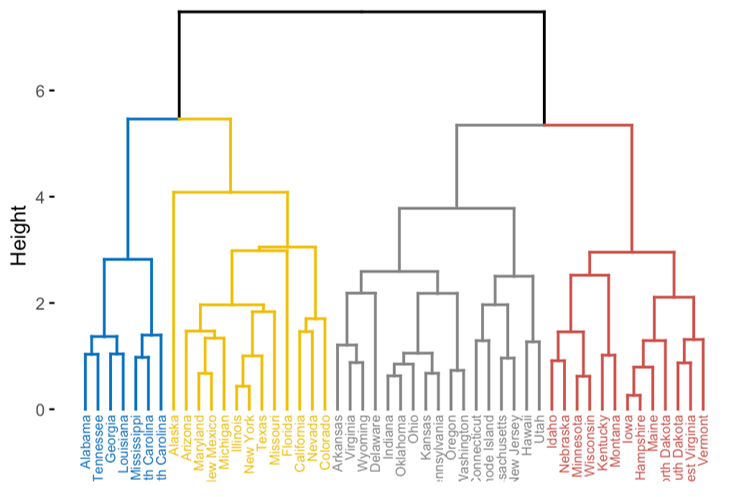
Hiearchical clustering의 결과 예시입니다. Height를 바탕으로 몇 개의 그룹으로 나뉘는 것을 확인할 수 있습니다.

Nested cluster and dendrogram

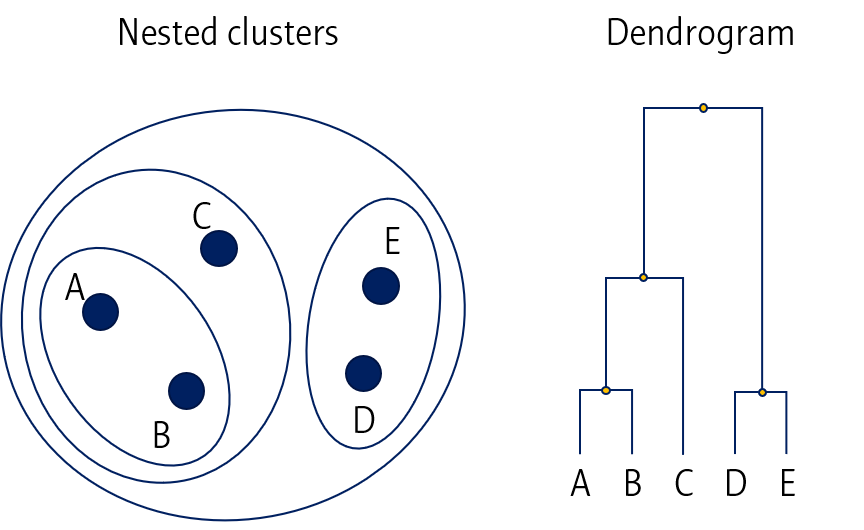
Hierarchical clustering 결과는 Nested cluster와 Dendrogram 두 가지 방법으로 시각화할 수 있습니다. 다만, Nested clustering는 데이터가 2D일 때만 효과적이기 때문에 주로 dendrogram을 이용합니다.

Overall procedure

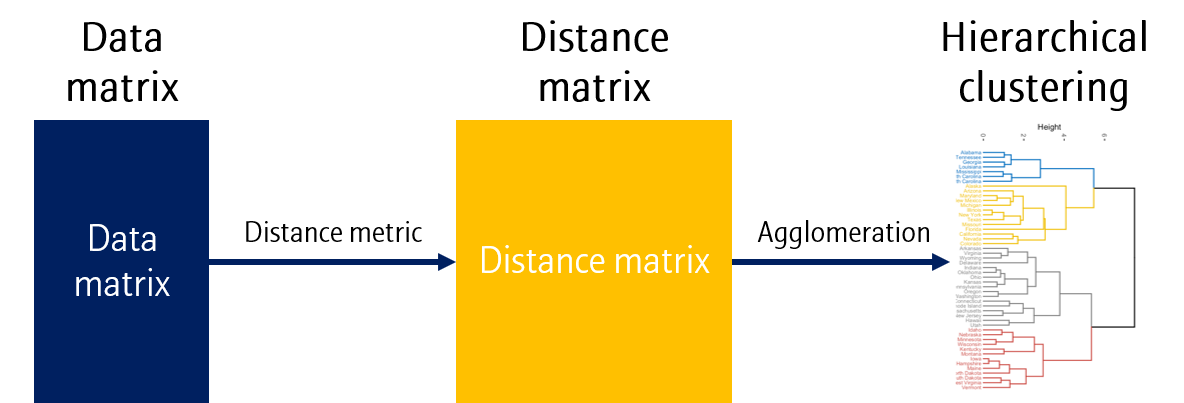
Hierarchical clustering은 위와 같이 데이터로부터 Distance matrix (또는 dissimilarity라고도 합니다)를 만든 뒤, Agglomeration (결합) 과정을 거쳐 dendrogram을 그립니다.

Distance metric과 Agglomeration에 사용되는 방법이 여러가지가 있습니다. Dendrogram 그리는 법 이전에 이 부분에 대해 먼저 정리해봅시다.

Distance metric

Distance라는 것은 데이터와 데이터 간 유사도의 역수 정도로 생각할 수 있습니다. 즉, 더 유사한 데이터간 Distance가 더 작게 나타납니다.

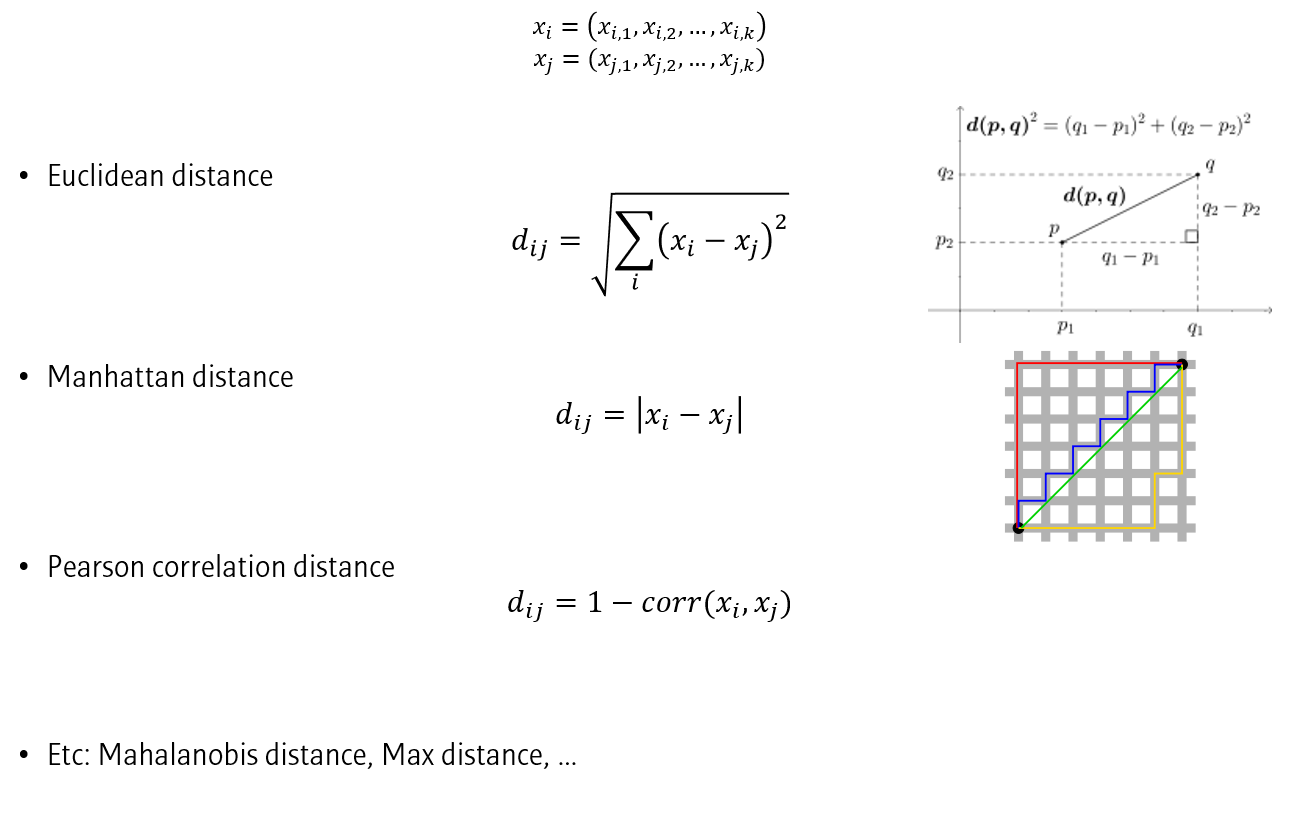
Distance를 측정하는 방법으로는 Euclidean distance (L2 distance), Manhattan distance (L1 distance), Pearson’s correlation distance 등이 있습니다.

Distance마다 수식이 다르지만, 결과적으로 두 데이터간의 차이를 수식화하고 있다는 것을 알 수 있습니다.

Distance matrix

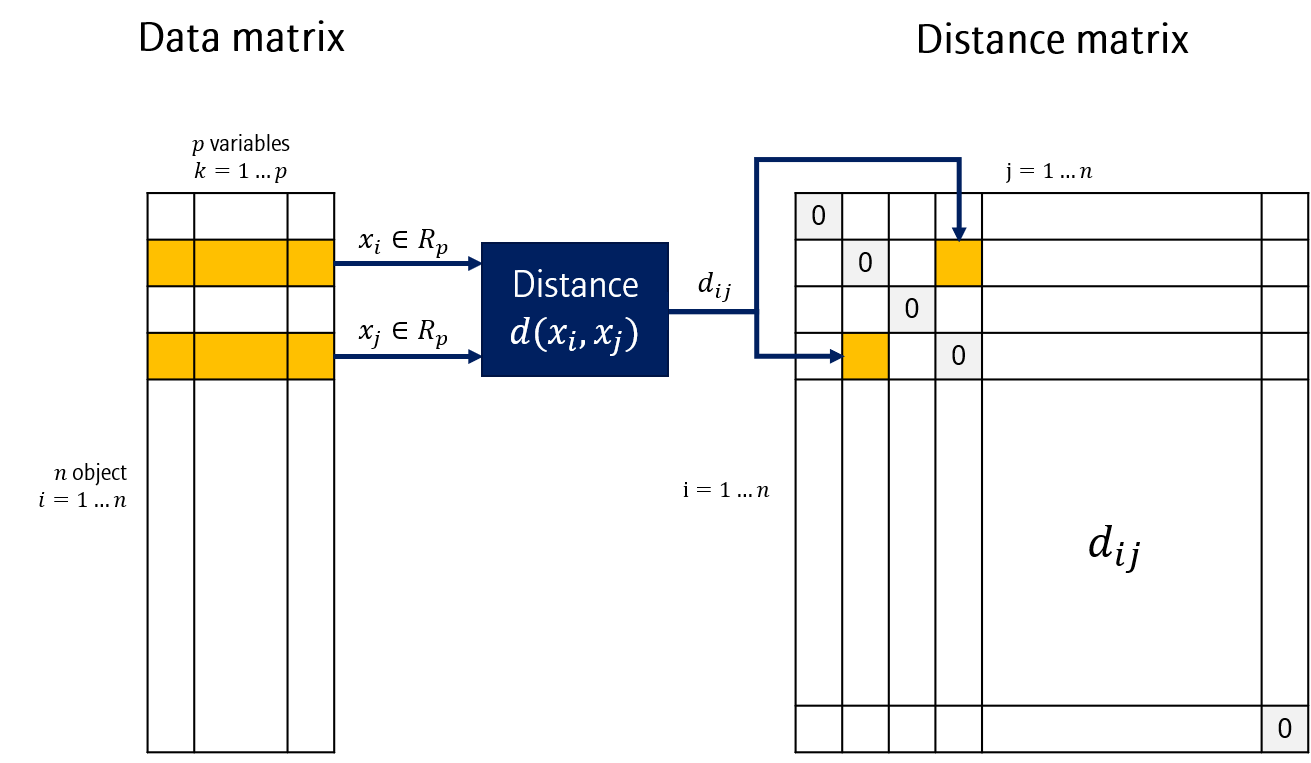
Data matrix에 \(n\)개 데이터가 \(p\)차원에 걸쳐 있다고 할 때 \(\frac{n(n-1)}{2}\)개의 (\(i, j\)) 쌍이 나올 수 있습니다. 모든 쌍에 대해 distance를 계산합니다. 이 결과를 테이블로 정리한 것을 Distance matrix라고 합니다. 모든 \(i, j\)에 대해 distance를 계산하기 때문에, matrix는 정사각형 모양을 띕니다. 또한 diagonal 항은 0 값을 가지며, diagonal에 대해 symmetric합니다.

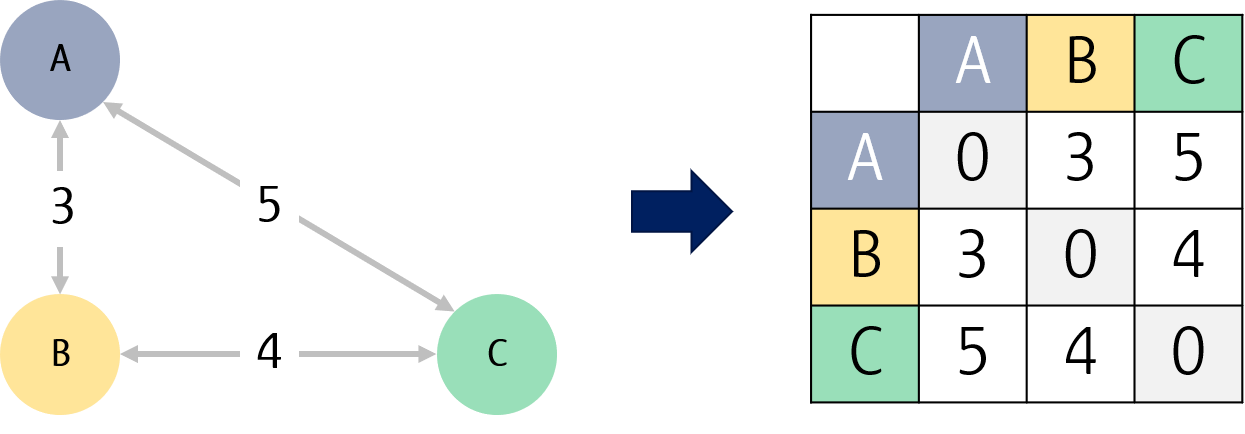
예를 들어 세 데이터 A, B, C는 총 3개의 distance를 가지며, A-B, B-C, A-C 거리가 각각 3, 4, 5일 때, distance matrix는 3x3 행렬로 나타낼 수 있습니다.

Types of hierarchical clustering

이제 Distance matrix는 구했고, Agglomeratio 과정을 정리해봅시다.

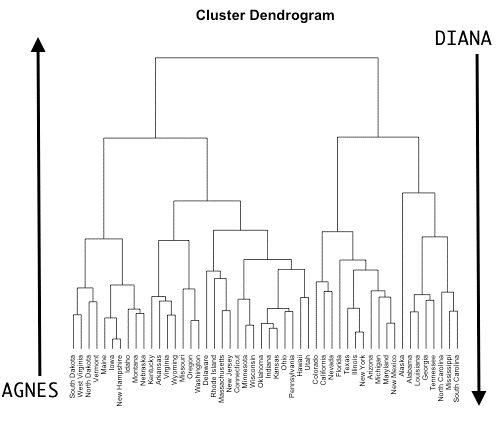
Hierarchical clustering은 AGNES (AGglomerative NESting, Bottom-up approach)와 DIANA (DIvise ANAlysis, Top-down approach)으로 나눌 수 있습니다.

AGNES는 각 데이터로부터 군집을 만들며, 그 군집을 점차 키워나가는 방식이고, DIANA는 반대로 군집을 점차 쪼개나가는 방식입니다. 본 포스팅에서는 AGNES 방식에 대해서 정리해보도록 하겠습니다.

Agglomeration

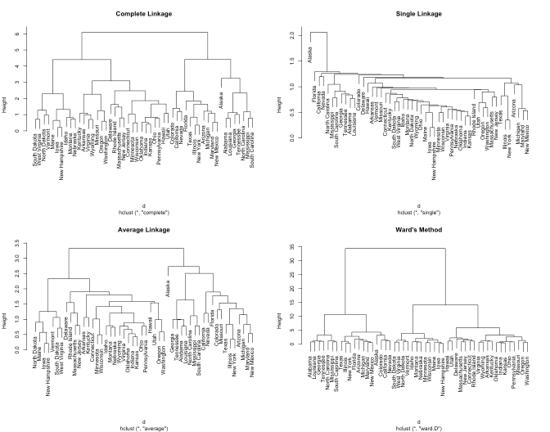
데이터와 데이터간의 거리를 계산하는 법은 위에서 정리했습니다. 그렇다면 군집과 군집 간의 거리는 어떻게 계산할까요? 이 계산 방법을 Linkage라고 합니다. 동일한 데이터라고 하더라도, Linkage 종류에 따라 위와 같이 완전히 상이한 결과를 보여줍니다.

Linkage methods

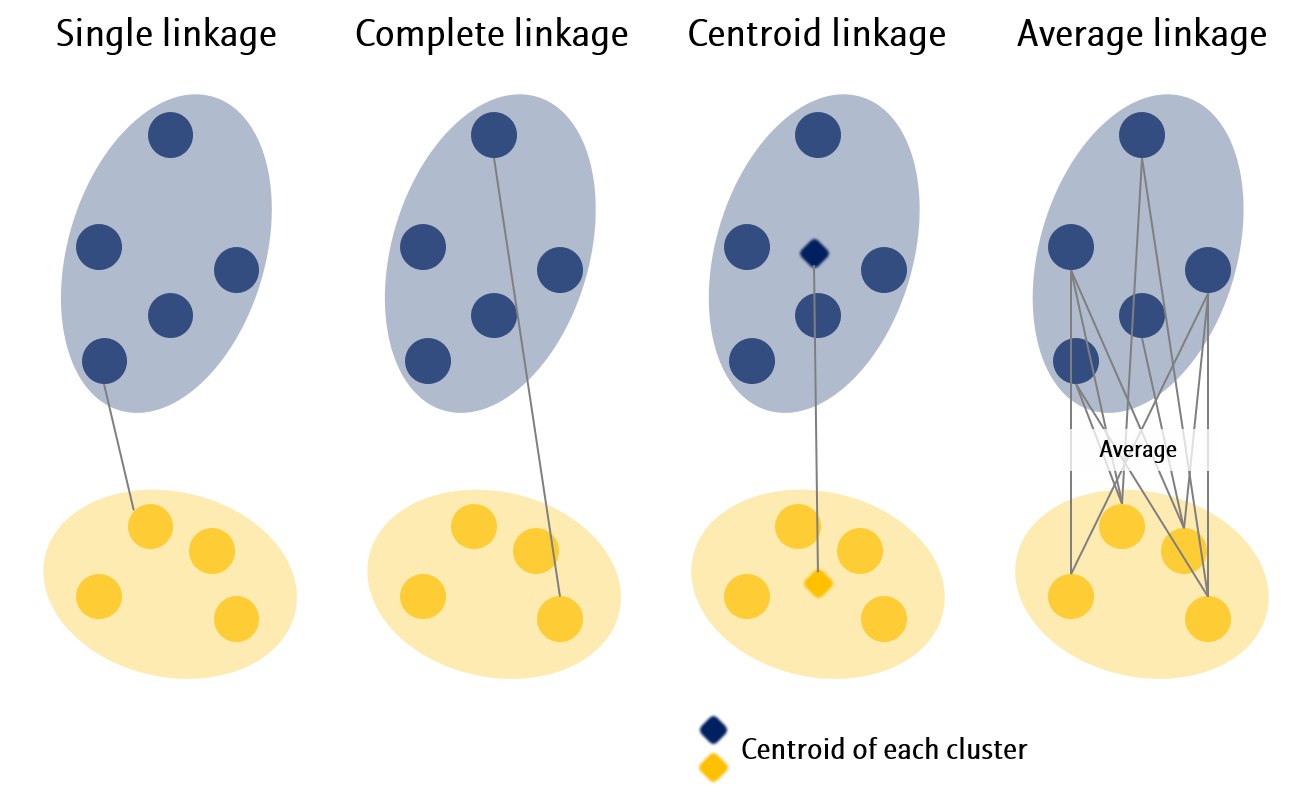
대표적으로 사용되는 몇 가지 Linkage 방법들입니다.

• Single linkage: 서로다른 군집의 모든 데이터 간 거리 중 최소값
• Complete linkage: 서로다른 군집의 모든 데이터 간 거리 중 최대값
• Centroid linkage: 서로다른 군집의 모든 데이터의 평균 (centroid) 간 거리
• Average linkage: 서로다른 군집의 모든 데이터 간 거리의 평균

Procedure

이제 Agglomerative hierarchical clustering 방법을 정리해봅시다.

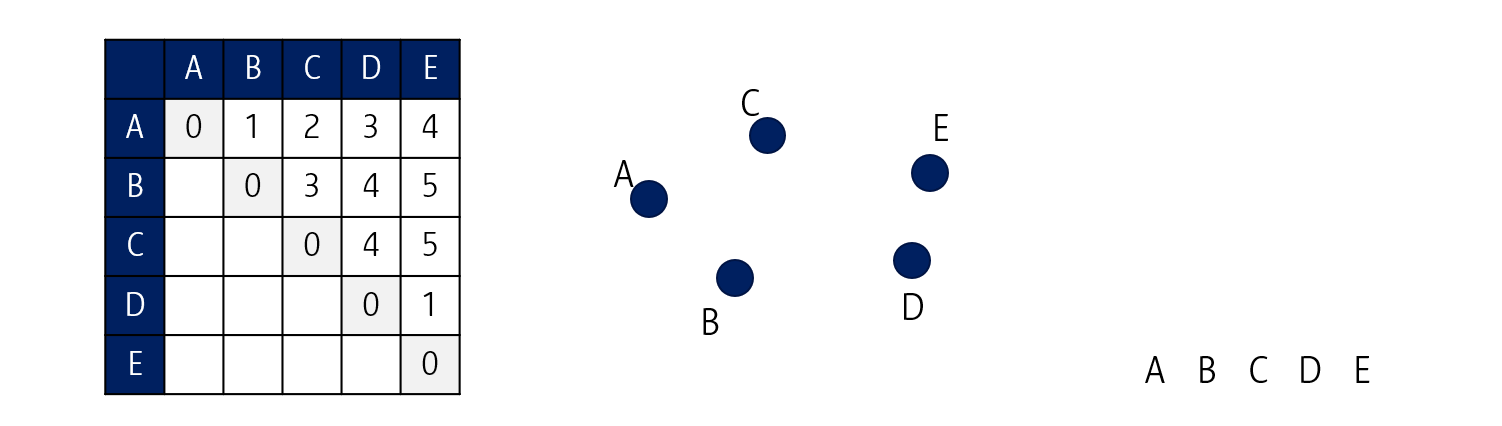
위와 같이 A, B, C, D, E 다섯 개의 데이터가 있고, 각 데이터간 거리는 좌측의 표와 같다고 해봅시다.

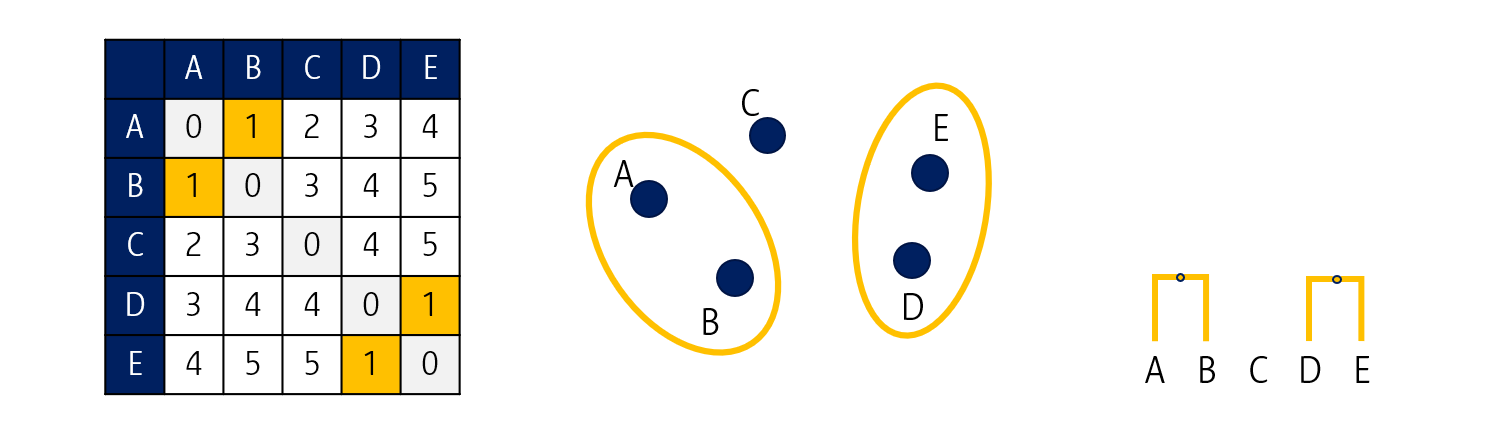
A-B 그리고 D-E 거리가 가장 짧으니 각각을 군집으로 묶습니다. 이 때 dendrogram의 높이는 군집 (데이터) 간 거리가 됩니다.

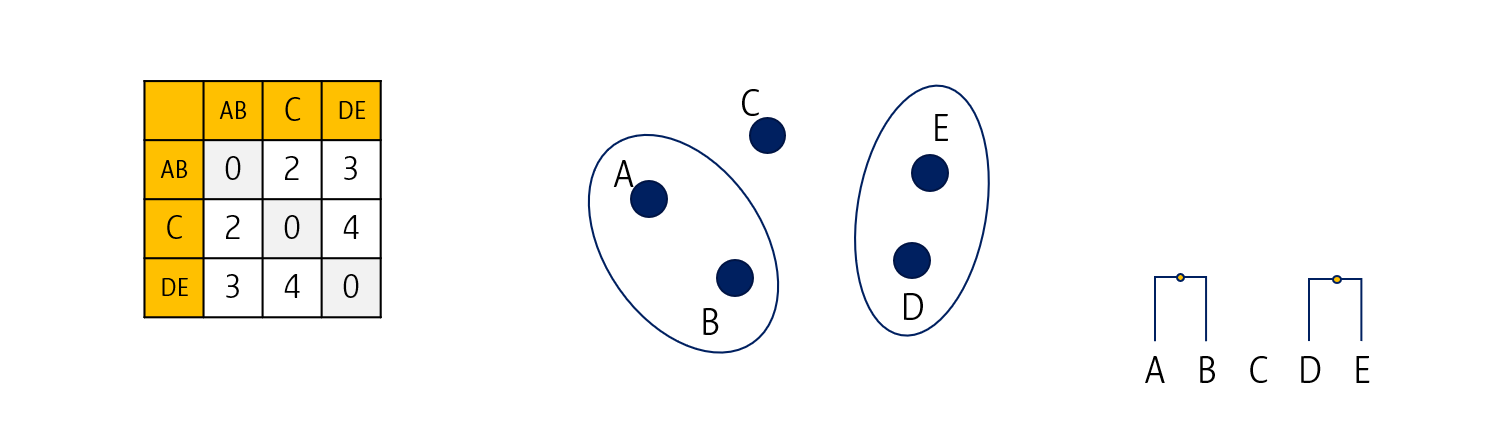
그러면 이렇게 첫 번째 군집이 완성됩니다. 이제 AB, C, 그리고 DE 간 거리를 다시 계산해서 distance matrix를 업데이트 합니다.

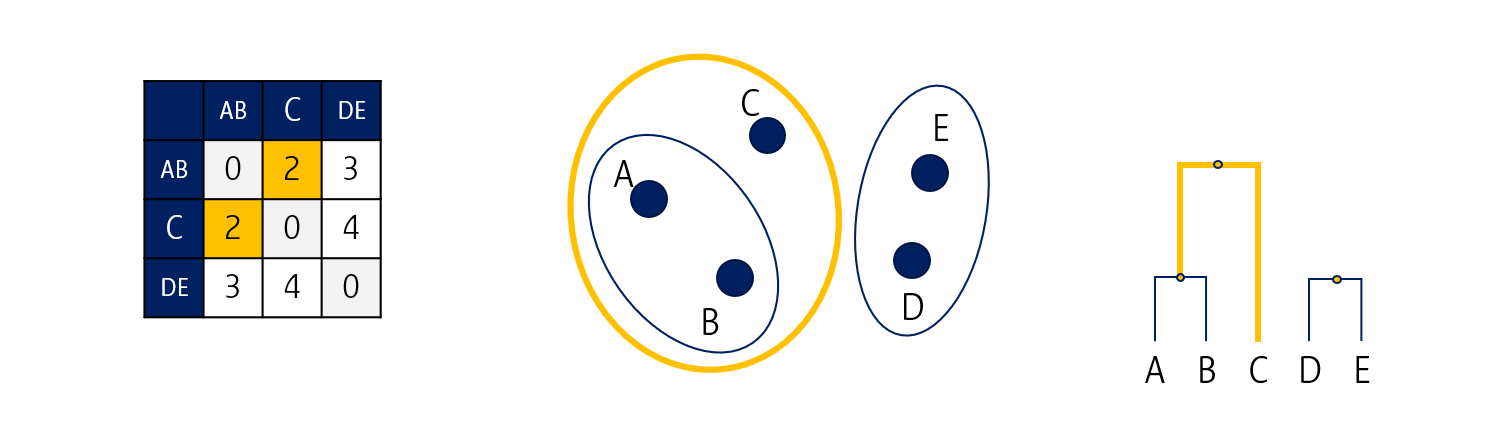
AB-C의 거리가 가장 가깝습니다. 이를 한 군집으로 묶어줍니다.

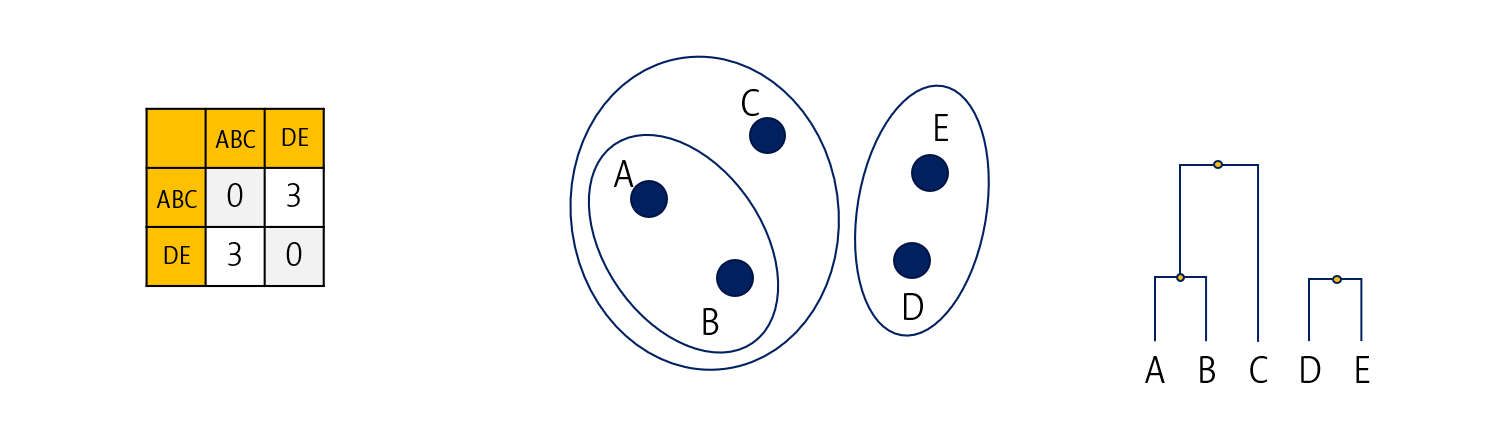
위의 과정을 반복해줍니다.

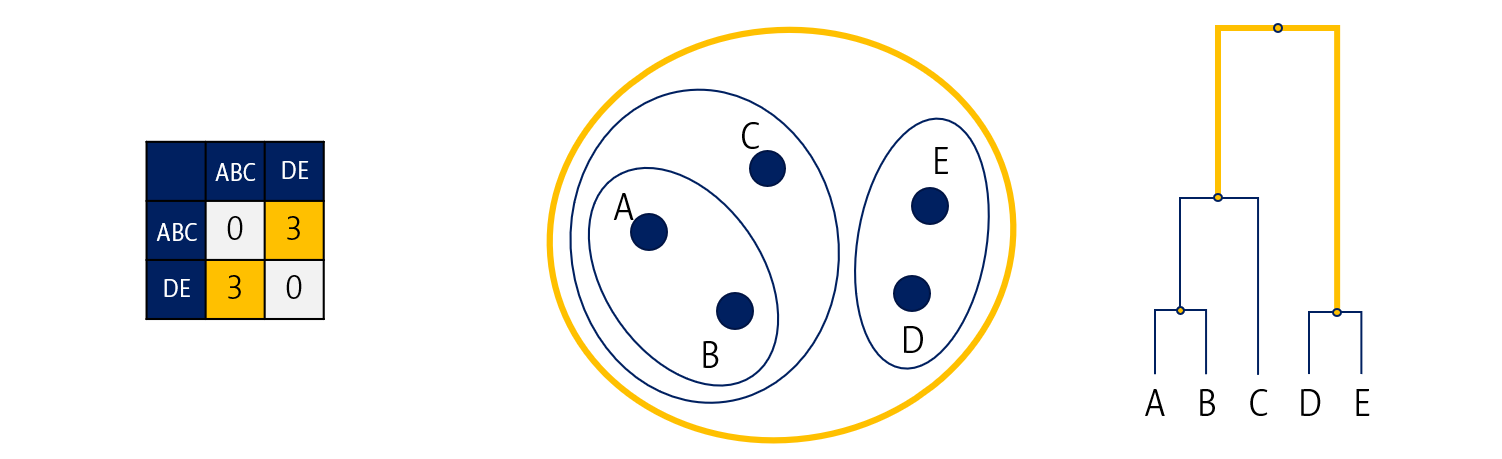
영차-영차

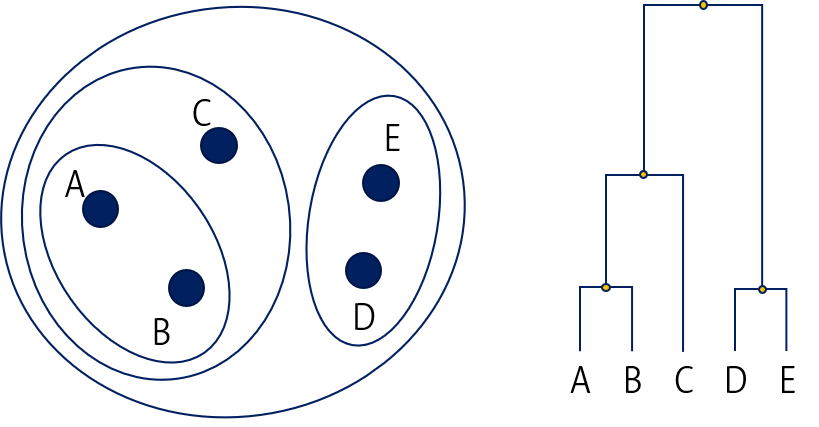
결과적으로 모든 데이터가 하나의 군집으로 합쳐지게 되면 끝납니다.

Number of clusters (k)

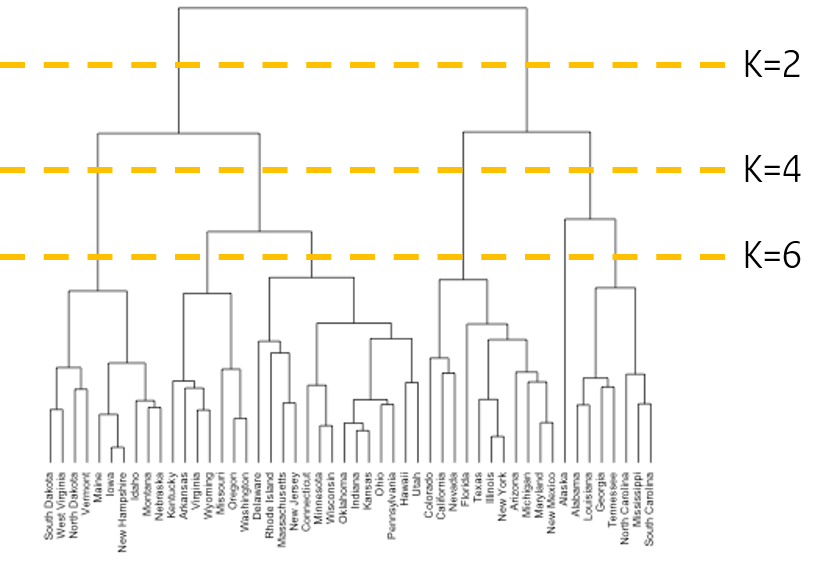
Hierarchical clustering에서는 K-means와 달리 군집의 개수를 사전에 설정하지 않습니다. 그 대신 최종 dendrogram에 가상의 선을 그어 몇 개의 군집으로 나눕니다. 그리고 이렇게 Clustering을 했을 때의 Dunn index, silhouette index 등의 metric (참고)을 통해 군집의 개수를 결정합니다.

---

앞서 말한 바와 같이, Hierarchical clustering은 뇌 연결성 분석이나 유전체 분석에 많이 사용됩니다.

다음 포스팅에서는 Self-organizing map (SOM) 또는 뇌 데이터에서의 HC기반 Connectivity 분석방법을 정리해보고자 합니다

다음 포스팅: 작성중