K-means clustering

October 31, 2020 Machine learning

이전 포스팅에서는 군집화 (Clustering)의 기본 개념에 대해 정리했습니다. 이번 포스팅에서는 Hard, Partitional 특징을 갖는 K-means clustering을 정리해보고자 합니다.

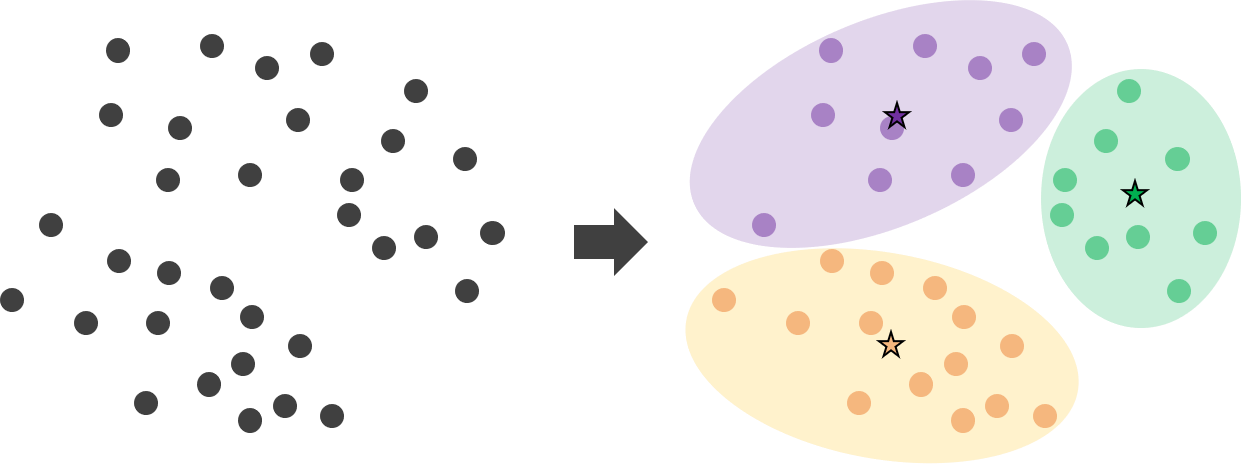
K-means clustering은 대표적인 군집화 기법입니다. 위 그림과 같이 각 클러스터가 생길 때, 클러스터 내 데이터의 평균값이 중요한 역할을 합니다.

알고리즘이 그렇게 복잡하지 않아 이해하기 쉽습니다.

K-means 알고리즘은 EM 알고리즘입니다. EM은 Expectation-Maximization 의 약자로, Expectation과 Maximization을 반복해나가며 데이터 분포를 학습하는 알고리즘을 말합니다.

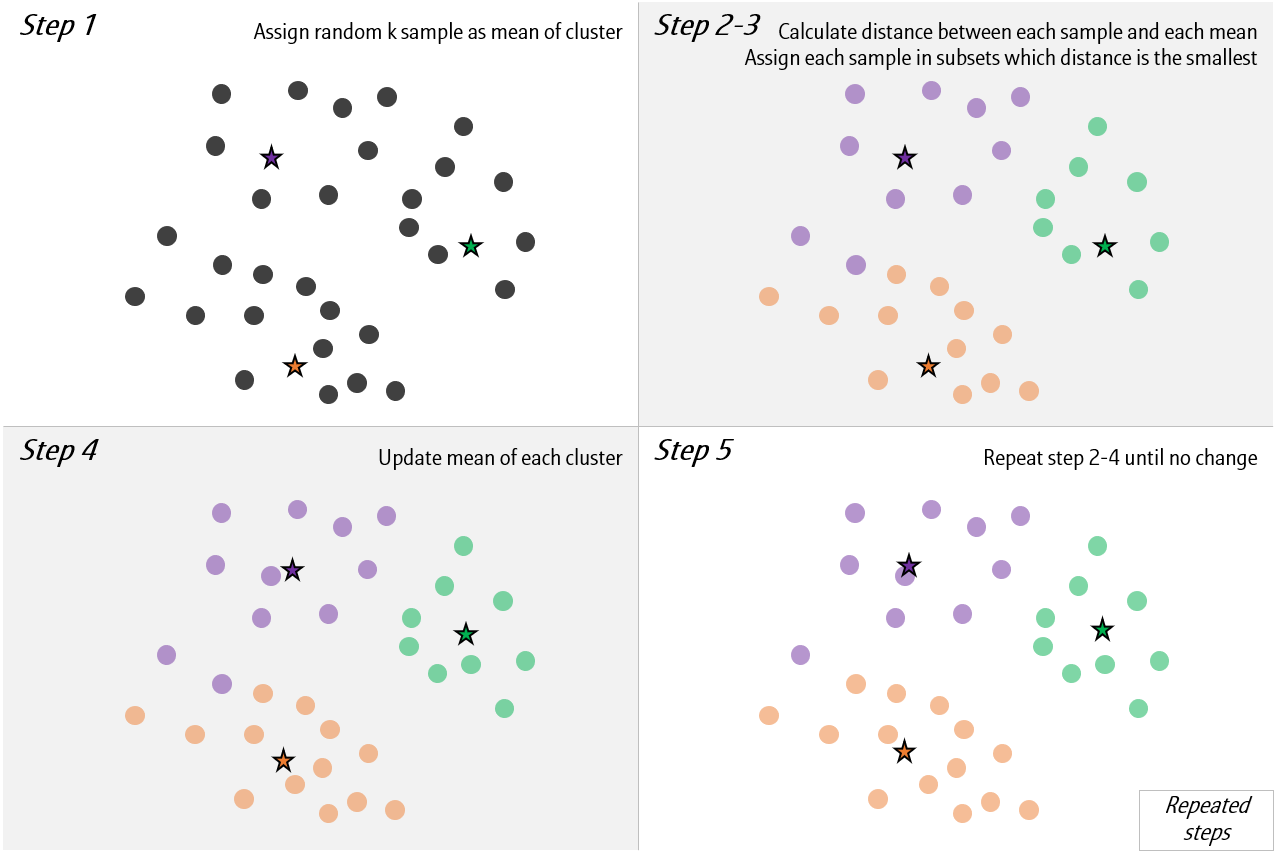
그림으로 보면 위와 같습니다. 원은 각 데이터를, 별은 클러스터의 평균을 의미합니다.

평균을 계산하고, 거리를 계산한 뒤, 가장 가까운 곳으로 데이터를 할당하는 과정을 반복합니다.

k-means 알고리즘은 k를 사전에 지정해줍니다. k에 따라 위와 같이 결과가 바뀌게 됩니다. 적절한 k는 이전 포스팅에서 살펴본 Dunn index나 Silhouettes 등을 이용하여 결정합니다.

Cons of K-means clustering

K-means clustering은 몇 가지 단점이 있습니다.

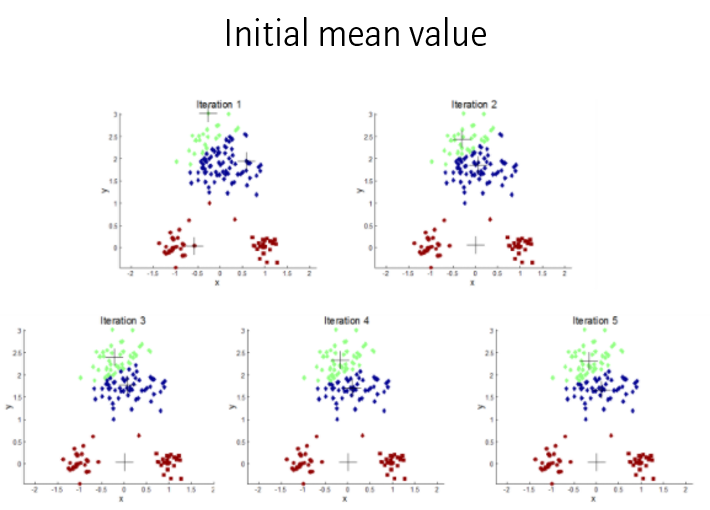
2020-10-31-k-means-clustering-4-cons-1-initial-value.png

첫째로 초기값 설정에 영향을 많이 받습니다. 위 예시와 같이 일부 초기값에 따라 클러스터링 결과가 이상하게 되는 경우가 있습니다.

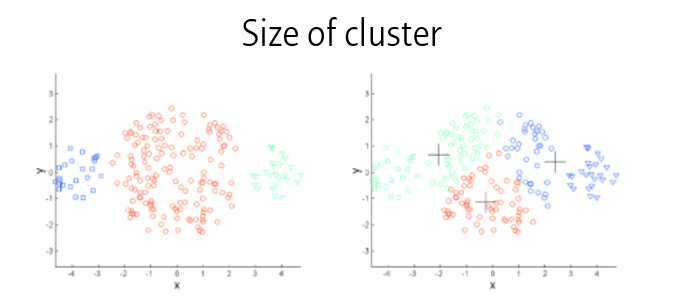
2020-10-31-k-means-clustering-5-cons-2-size-of-cluster.png

둘째로 클러스터의 사이즈에 영향을 받습니다.

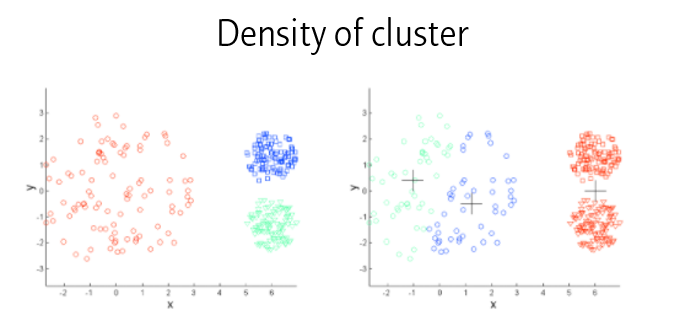
2020-10-31-k-means-clustering-6-cons-3-density-of-cluster.png

마찬가지로 클러스터의 밀도에도 영향을 받습니다.

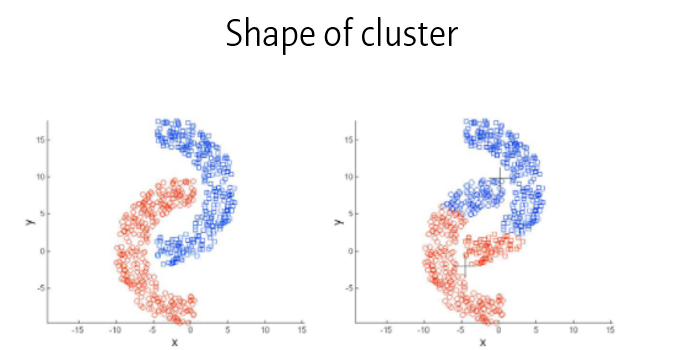
2020-10-31-k-means-clustering-7-cons-4-shape-of-cluster.png

마지막으로 데이터의 분포에 따라서도 영향을 받습니다.

다음 포스팅에서는 Hierarchical clustering을 정리해보고자 합니다