Machine learning: Odds와 Log(Odds)

Odds와 Log(odds)의 개념을 정리해봅시다.

StatQuest의 StatQuest: Odds and Log(Odds), Clearly Explained!!! 강의를 참고했습니다.

Odds

Odds는 임의의 사건 A가 발생하지 않을 확률 대비 일어날 확률의 비율입니다. 확률과 비슷하지만 조금 다릅니다 (후술)

\[ odds=\frac{P(A)}{P(A^c)}=\frac{P(A)}{1-P(A)} \]

Odds example 1

5번의 경기 중, 우리 팀이 1번을 이겼다고 할 때 Odds는 아래와 같이 0.25로 계산됩니다.

\[ odds=\frac{P(A)}{1-P(A)}=\frac{1}{4} \]

Odds example 2

이번에는 8번의 경기 중, 우리 팀이 5번을 이겼다고 할 때 Odds는 아래와 같이 1.7로 계산됩니다.

\[ odds=\frac{P(A)}{1-P(A)}=\frac{1}{4} \]

Odds VS Probability

주의할 점은 위에서 언급한 것과 같이 Odds와 확률 (probability)는 다르다는 것입니다.
odds는 사건 A가 일어날 확률 / 일어나지 않을 확률인 반면, probability는 사건 A가 일어날 경우의 수 / 전체 경우의 수로 표현됩니다.

동일한 예시 2에서 odds는 1.7, probability는 0.625의 값을 갖는 것을 확인할 수 있습니다.

Log(Odds)

Odds는 그대로 사용하기보다 오즈비 \(Odds\; ratio\) 또는 로짓 \(Log(odds)\)으로 사용하는 경우가 많습니다.

Asymmetric odds

Odds의 단점은 Asymmetric하다는 점입니다.

이를 이해하기 위해, 예시를 살펴봅시다.

경기에서 1번 이기고 1번 지는 경우, \(odds=\frac{1}{1}=1\)입니다.
우리 팀이 좀 못해서, 1번 이기고 5번 지는 경우, \(odds=\frac{1}{5}=0.2\)입니다.
우리 팀이 많이 못해서, 1번 이기고 10번 지는 경우, \(odds=\frac{1}{10}=0.1\)입니다.
우리 팀이 진짜 너무 못해서, 1번 이기고 50번 지는 경우, \(odds=\frac{1}{50}=0.02\)입니다.
우리 팀이 정말 나락 그 자체라, 1번 이기고 100번 지는 경우, \(odds=\frac{1}{100}=0.01\)입니다.

이번에는 긍정적인 예시를 들어봅시다.

경기에서 1번 이기고 1번 지는 경우, \(odds=\frac{1}{1}=1\)입니다.
우리 팀이 좀 잘해서, 5번 이기고 1번 지는 경우, \(odds=\frac{5}{1}=5\)입니다.
우리 팀이 많이 잘해서, 10번 이기고 1번 지는 경우, \(odds=\frac{10}{1}=10\)입니다.
우리 팀이 진짜 너무 잘해서, 50번 이기고 1번 지는 경우, \(odds=\frac{50}{1}=50\)입니다.
우리 팀이 정말 천상계 그 자체라, 100번 이기고 1번 지는 경우, \(odds=\frac{100}{1}=100\)입니다.

문제점을 발견했습니다. 1WIN, 5LOSE의 odds는 0.2인 반면, 5WIN, LOSE의 odds는 5입니다. 두 값을 통해 결과를 직관적으로 이해하기 어렵습니다.

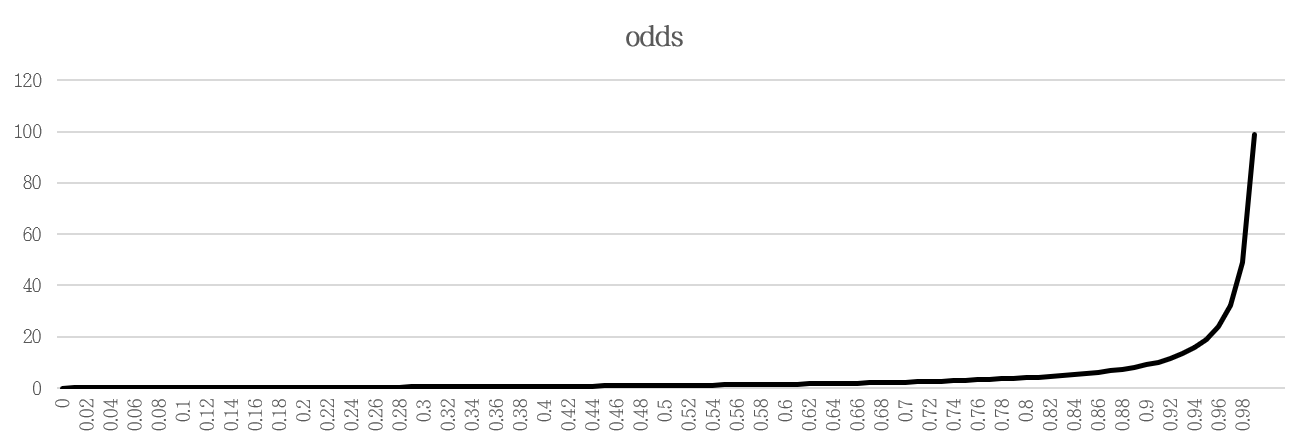
확률에 따른 Odds의 분포를 그려보았습니다. Odds는 P(A)가 0에 가까울수록 0 값을 가지며, 1에 가까울수록 커지면서 무한대로 발산합니다.

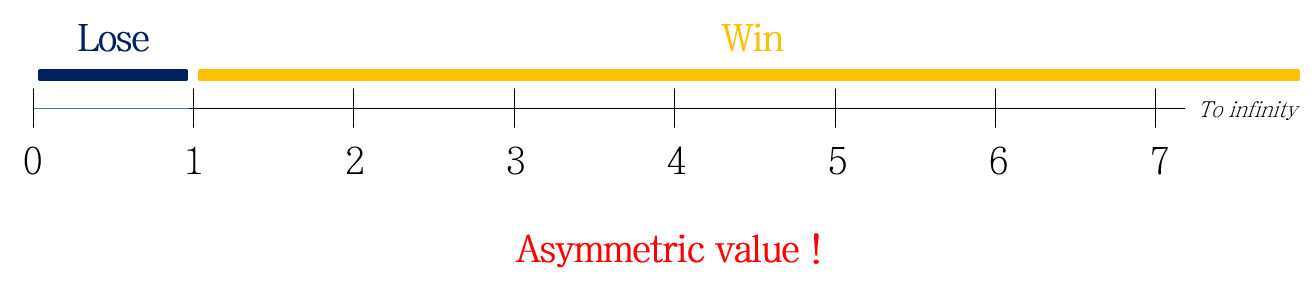
P(A)가 0.5보다 작을 때의 odds는 0~1에 분포되는 반면, 0.5보다 커지면 1부터 무한대까지 엄청난 범위를 차지합니다. 이는 해석할 때의 어려움뿐만 아니라, 수학적인 계산에서 문제를 낳습니다 (회귀 문제를 못 푸는 등)

Symmetric log(odds)

반면, Odds에 log 변환 (자연 로그)을 해준 logit은 0.5를 대칭으로 -무한대에서 무한대로 발산합니다.

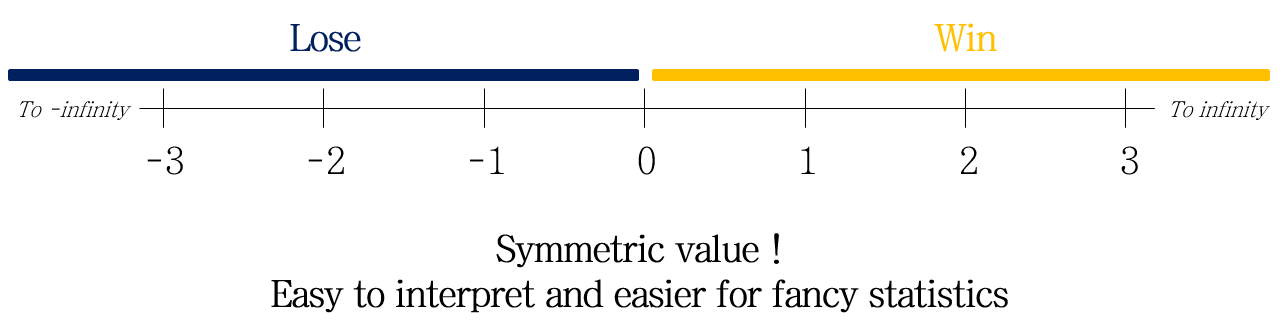
분포가 symmetric해진 것을 확인할 수 있습니다 ! 이제 회귀문제뿐 아니라, 여러 곳에 log odds를 적용 가능합니다.

위의 예시 중 몇 개만 뽑아보면, 1WIN, 5LOSE의 경우, \(odds=log\frac{1}{5}=-1.61\)인 반면, 5WIN, LOSE의 \(odds=log\frac{5}{1}=1.61\)입니다. 두 값이 0을 중심으로 대칭을 이루기 때문에 직관적으로 이해할 수 있습니다.