Machine learning: Bias(편향)과 Variance(분산)

이번 포스팅에서는Bias(편향)과 Variance(분산)을 정리해보겠습니다.

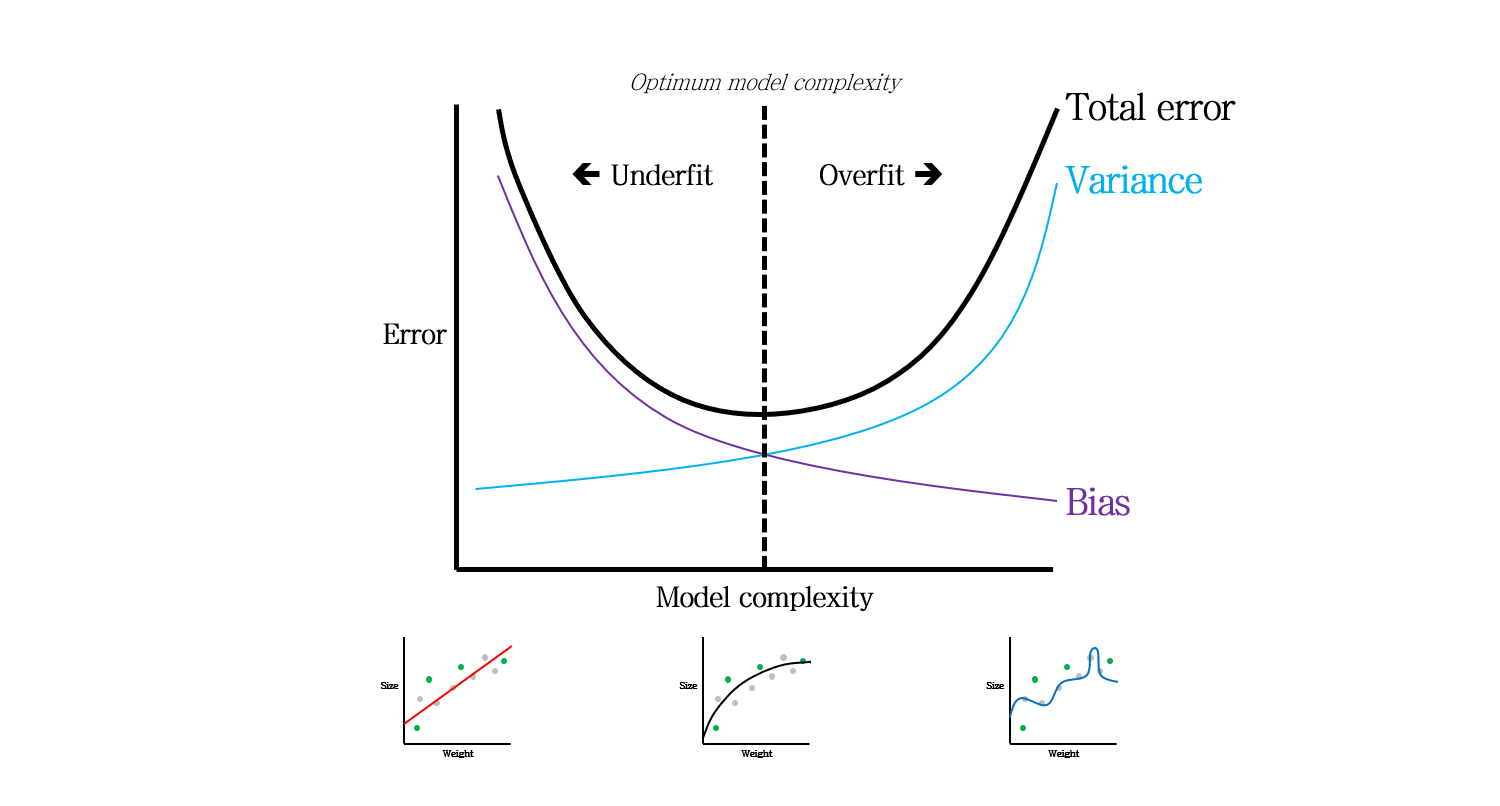
오늘 포스팅에서 정리할 최종 요약본입니다.

Bias(편향)과 Variance(분산)

Bias (편향)와 Variance (분산)은 기계학습에서 아주 중요한 개념들입니다. 그런데 막상 Bias와 Variance를 정의하려고 하면 조금 애매하게 느껴집니다.

예시를 통해 Bias와 Variance를 정리해봅시다. Machine Learning Fundamentals: Bias and Variance의 예시를 재구성했습니다.

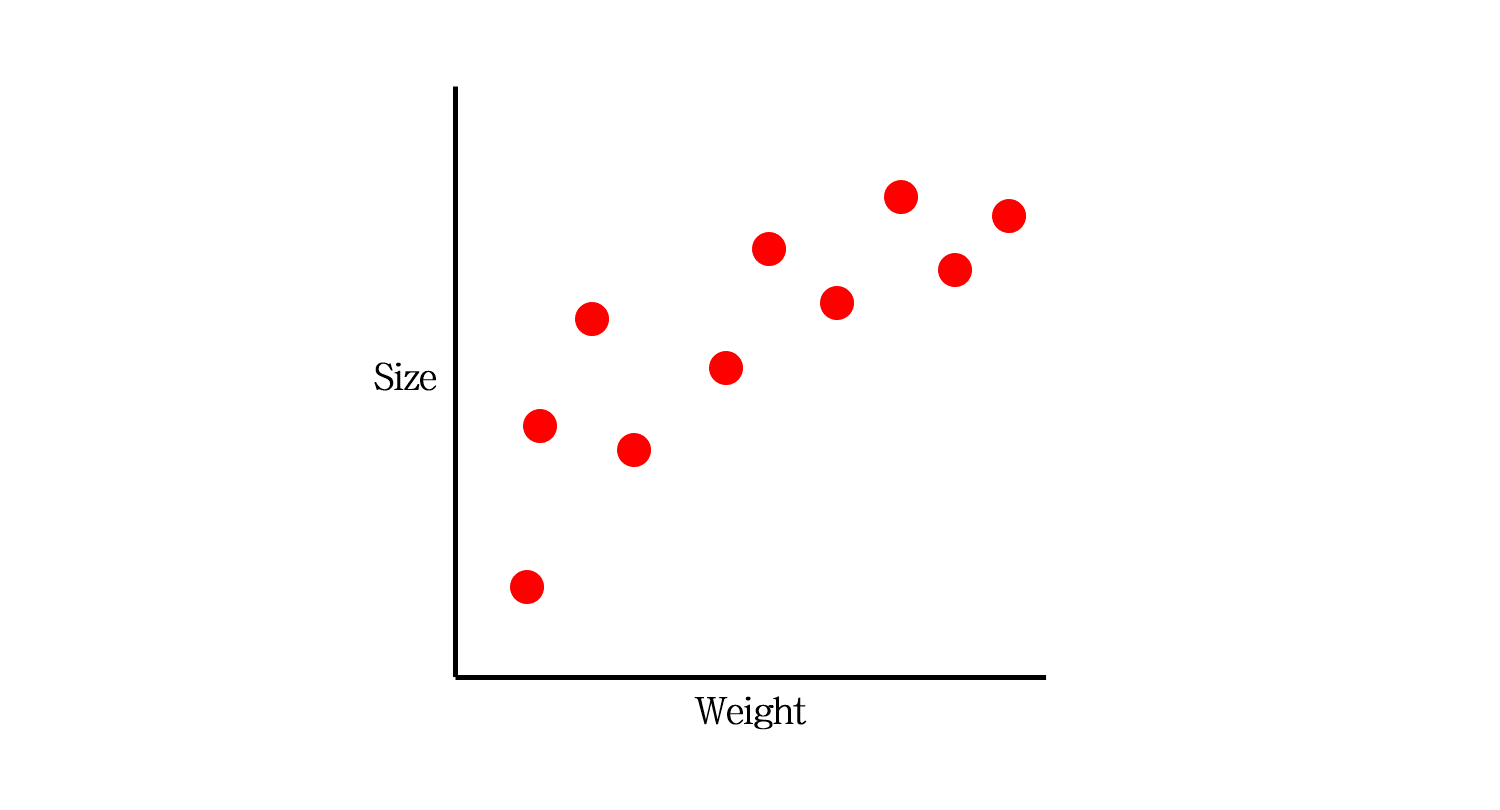
오늘 다룰 예시 데이터입니다. 쥐의 무게로 사이즈를 추정하는 모델을 만들고자 합니다.

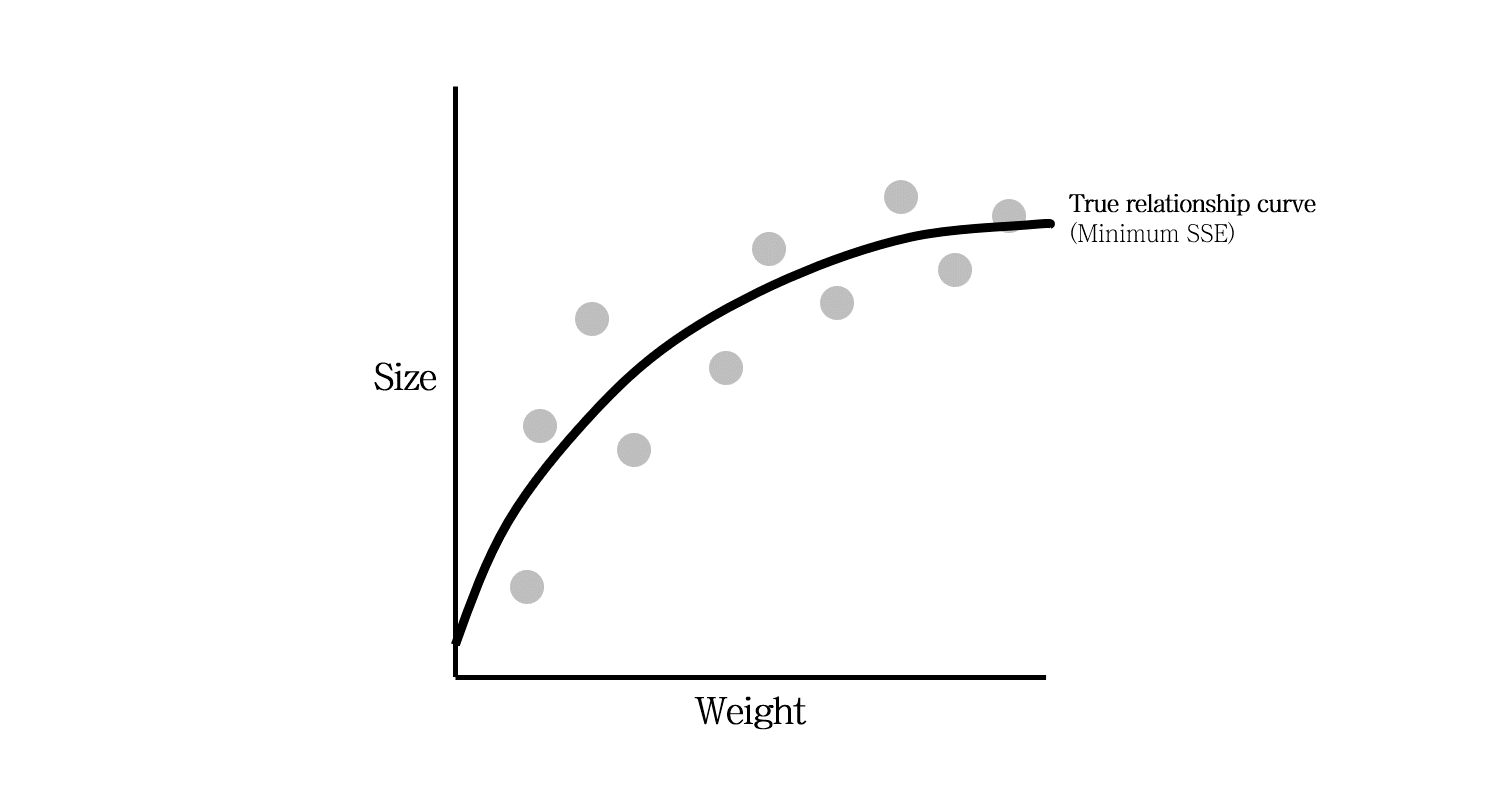
데이터를 완전히 이해하고 있다면 이렇게 약간 휜 log 모양의 모델을 만들 수 있을 것입니다. 하지만 현실은 녹록치 않습니다. 여러 모델을 테스트해보면서 최적의 모델을 찾아나가야 합니다.

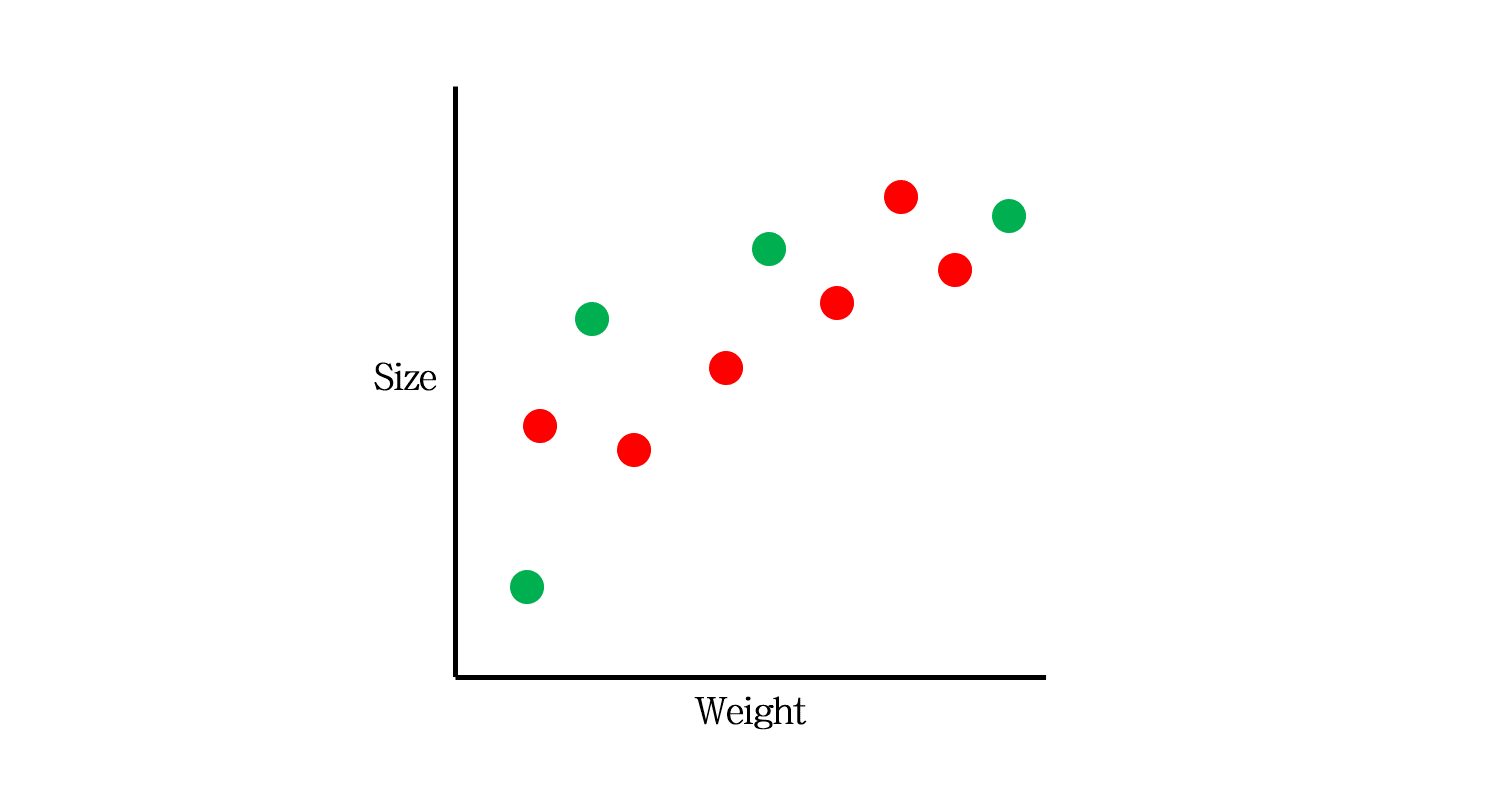
이를 위해 가장 먼저 하는 일은 데이터셋을 Training (빨간색)과 Test set (초록색)으로 분리하는 것입니다.

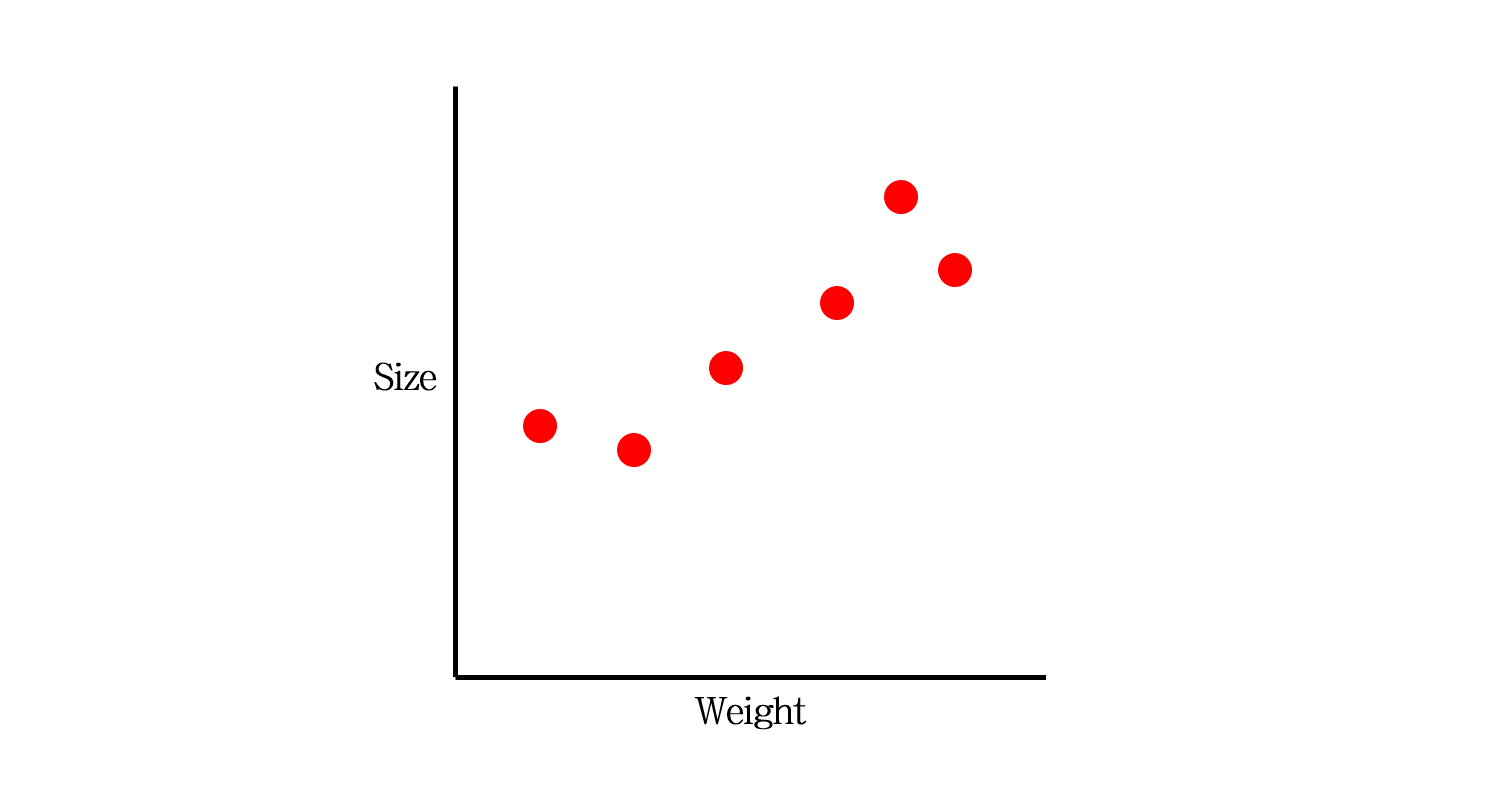
이 중 빨간색 Training data만을 갖고 모델을 만듭니다. 어떤 모델을 만들 수 있을까요?

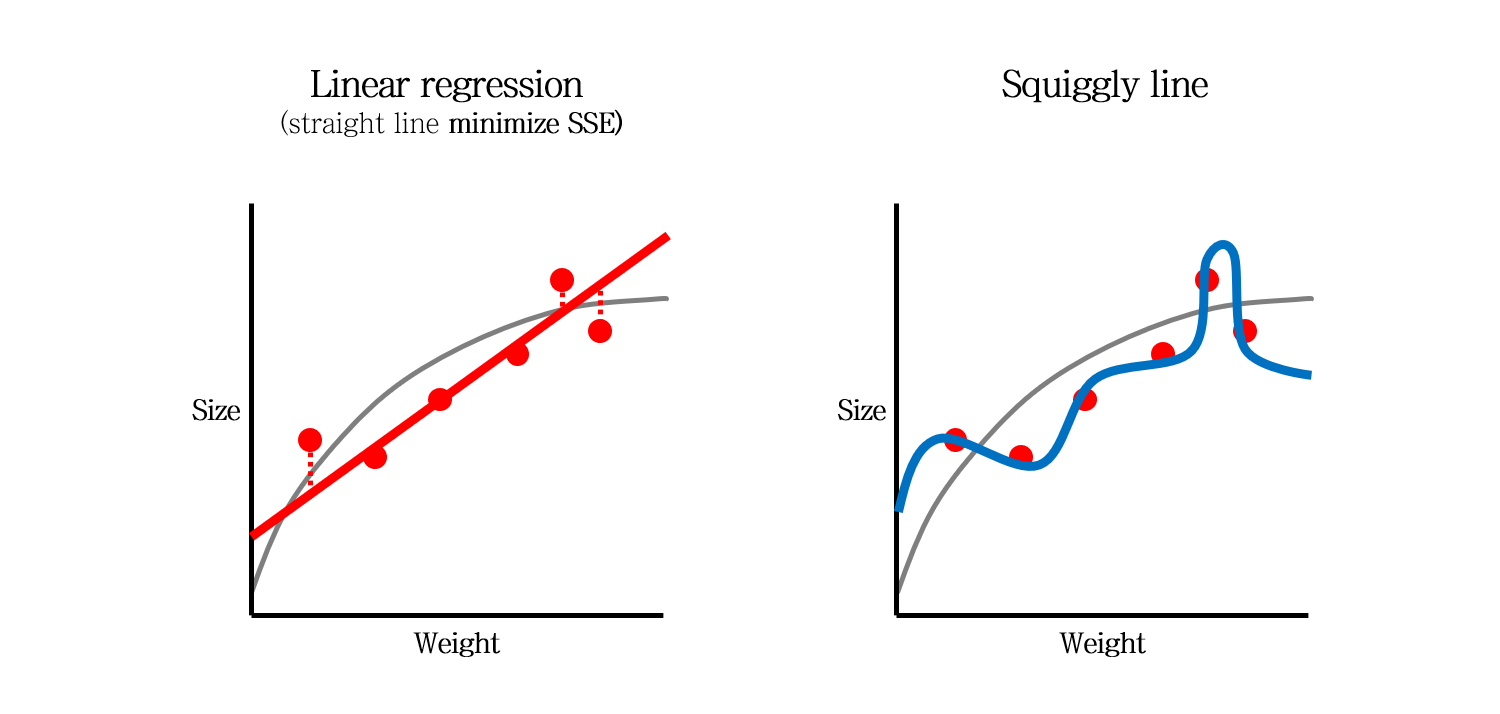
간단하게 두 가지의 모델을 생각해볼 수 있습니다. 좌측의 직선 모델과, 우측의 구불구불한 (Squiggly) 모델입니다.

좌측의 직선 모델은 SSE를 최소화하는 직선으로 만들어집니다. 그리고 우측의 구불구불한 모델은 SSE가 0이 되도록 만들어집니다.

Bias

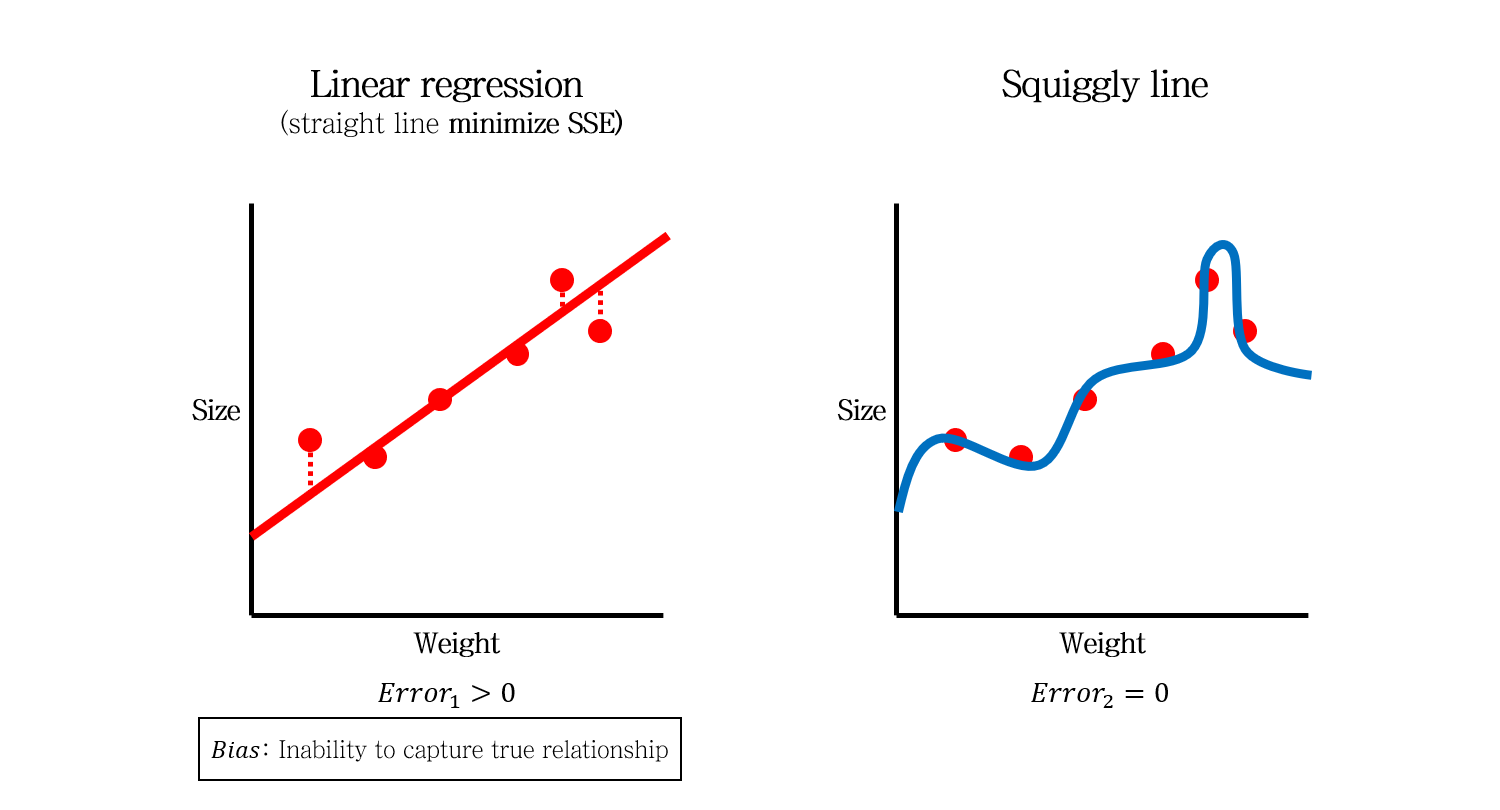
이 때, 직선 모델은 어떻게 해도 실제 모델인 log 형태의 모델을 만들 수 없습니다. 바로 이 차이 (모델과 실제 관계와의 차이 Error)를 Bias라고 합니다.

따라서, Bias의 측면에서는 구불구불한 모델이 직선 모델보다 더 좋은 모델이라고 할 수 있습니다.

Variance

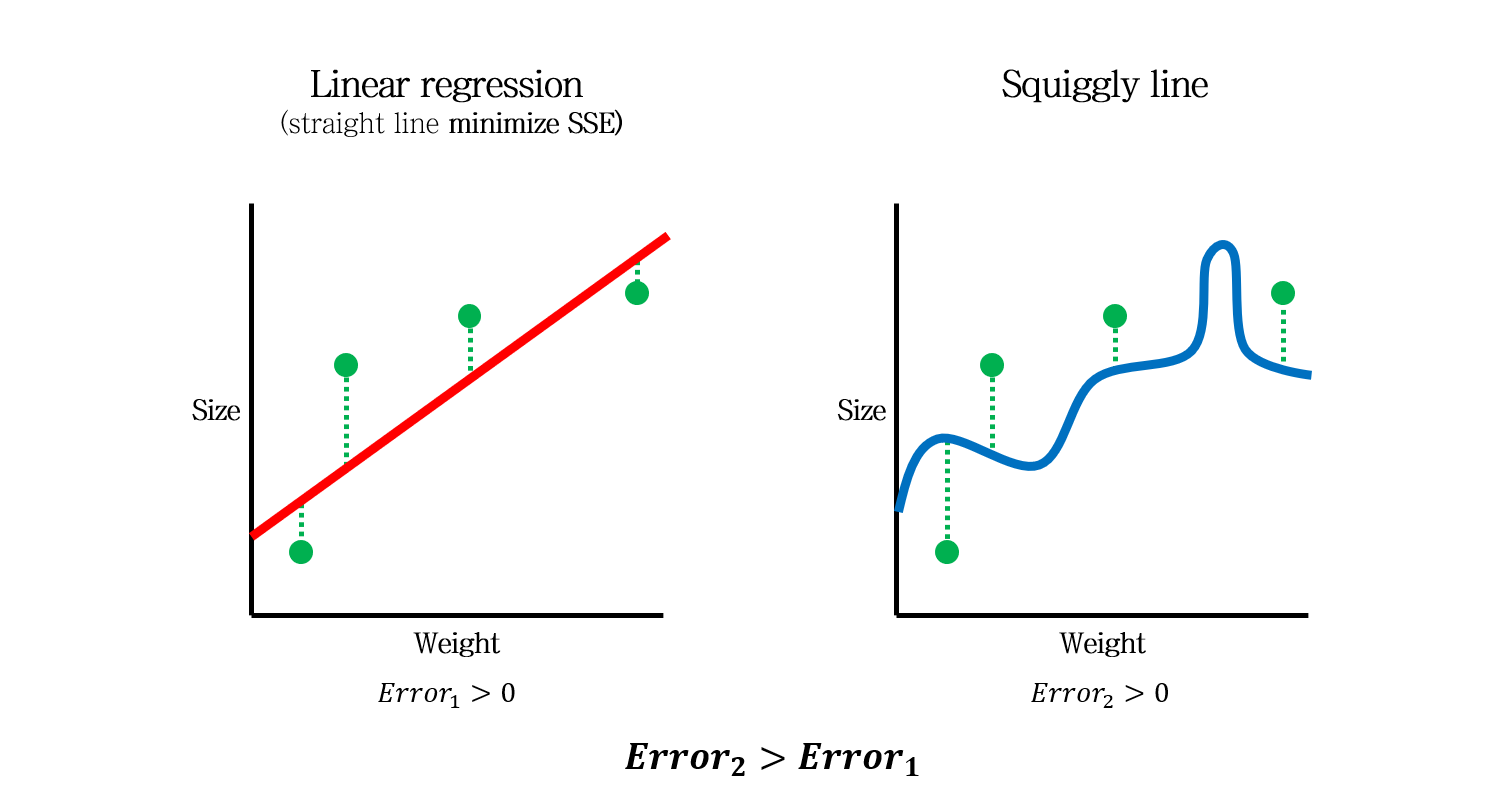
어찌저찌 두 모델을 만들었는데, Test data (초록색)을 새로 얻었습니다. 각 샘플의 Error를 통해 Test data의 SSE를 계산해보니, 구불구불한 모델의 SSE가 직선 모델의 SSE보다 더 큽니다.

따라서 Test data에 대해서는 직선 모델이 더 좋은 모델이라고 할 수 있습니다.

이 때, 데이터셋간의 차이에서 나오는 Error를 Variance라고 말할 수 있습니다.

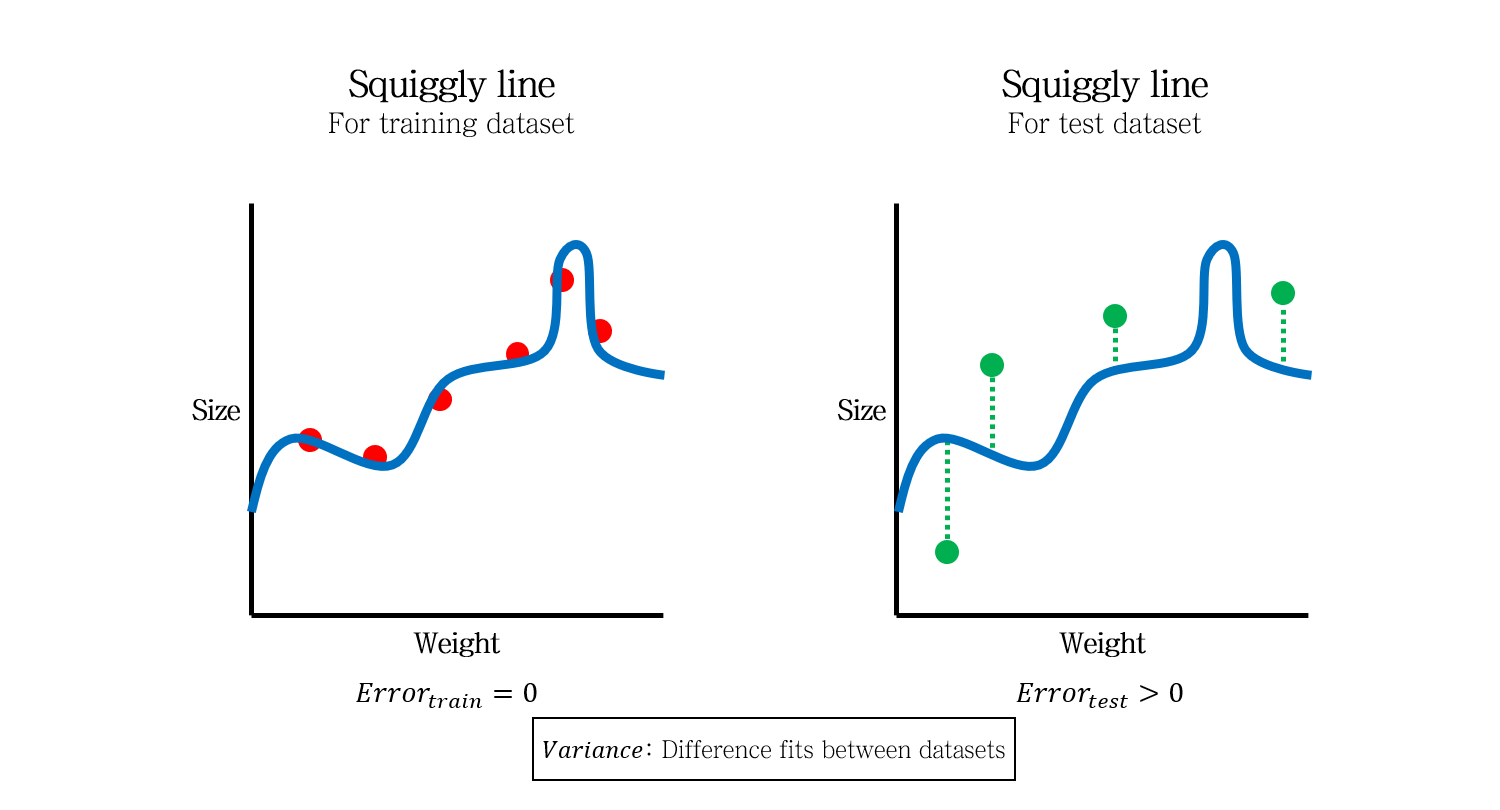
구불구불한 모델은 Training data에서는 Error가 0이었지만, Test data에 대해서는 큰 Error를 만들었습니다. 즉, Variance가 높은 모델이라고 할 수 있습니다.

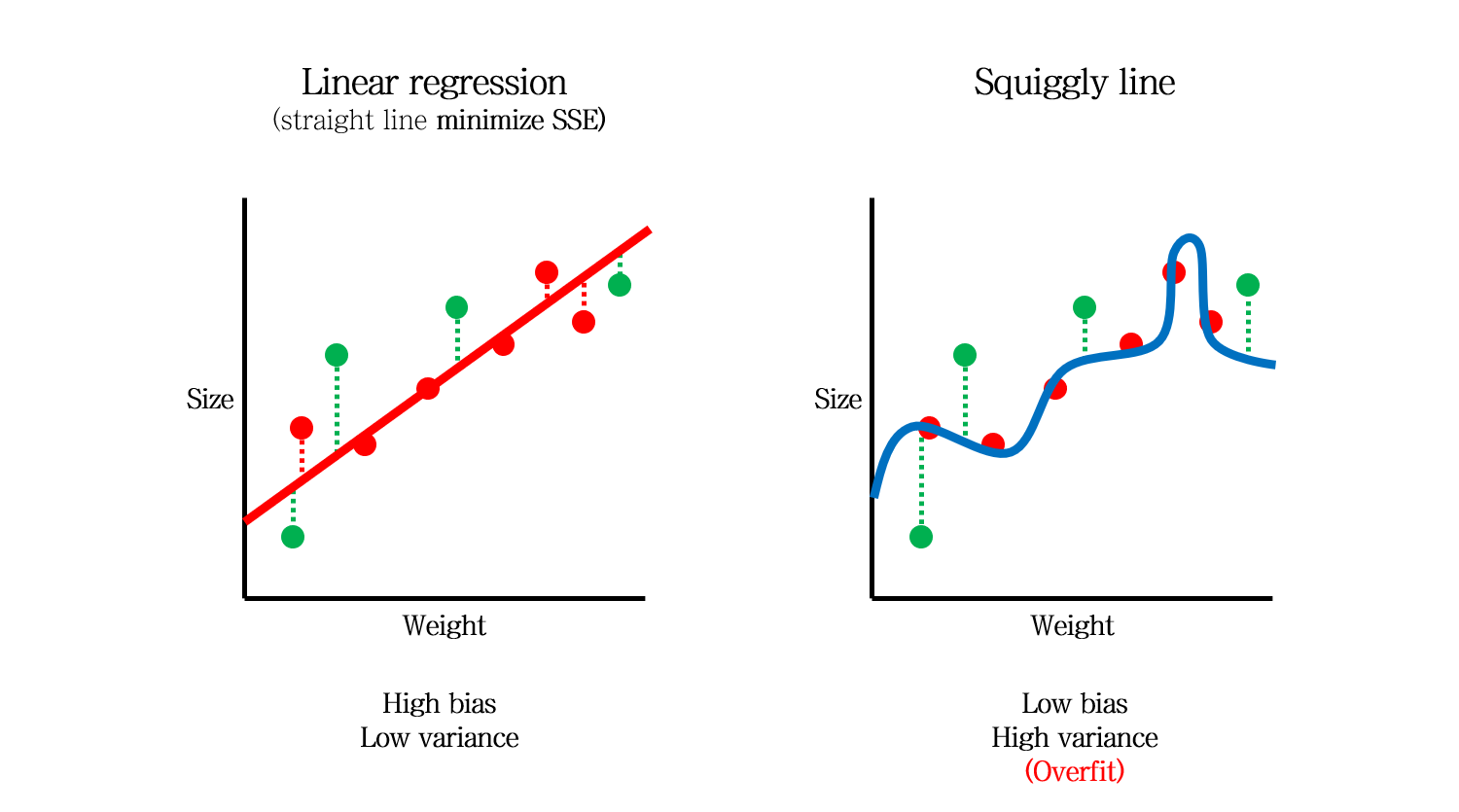
따라서 직선모델은 Bias는 높지만 Variance는 낮은 모델, 구불구불한 모델은 Bias는 낮지만 Variance가 높은 모델이라고 할 수 있습니다.

Underfitting과 Overfitting

예시의 구불구불한 모델과 같이 Bias는 낮지만 Variance가 높은 모델은 Overfit된 모델이라고 불립니다. Overfit된 모델은 Training data에 대해서는 높은 성능을 보이지만, Test data에 대해서는 확연히 떨어지는 성능을 보이는 특징을 갖습니다.

반대로 Underfit된 모델은 Training data에 대해서도 optimal한 경우보다 떨어지는 성능을 보입니다.

Bias-Variance Tradeoff

따라서 Bias와 Variance를 고려했을 때, 두 Error의 합인 Total error를 최소화시키는 모델이 주어진 데이터를 가장 잘 설명하는 모델이라고 말할 수 있습니다.