Segmentation for MEDIA (4) Graph model-based segmentation
이전 포스팅: Segmentation for MEDIA (3) Region growing & Wathershed algorithm
이전 포스팅에서는 사용자의 도움을 받아 ROI 영역을 분리해내는 Region growing과 Wathershed 알고리즘을 정리했습니다
이번 포스팅에서는 Graph model-based segmentation을 정리해보고자 합니다.
Graph model
Graph model은 foreground와 background를 분리하는 것을 보다 수학적으로 나타낸 모델이라고 할 수 있습니다.
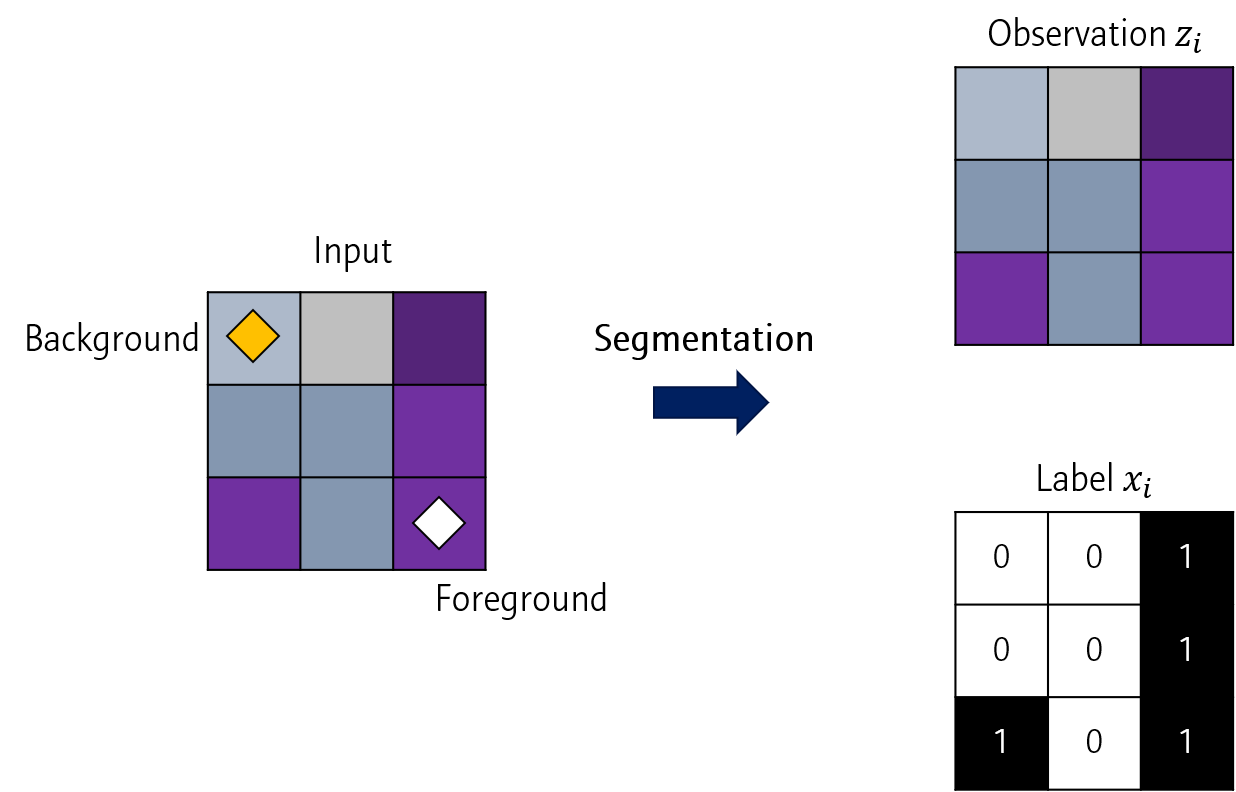
주어진 영상 이미지 (좌)의 보라색 부분을 Foreground라고 해봅시다. 이 이미지 자체는 Observation \(z_i\)로, 각 픽셀의 label 값은 \(x_i\)로 나타낼 수 있습니다.
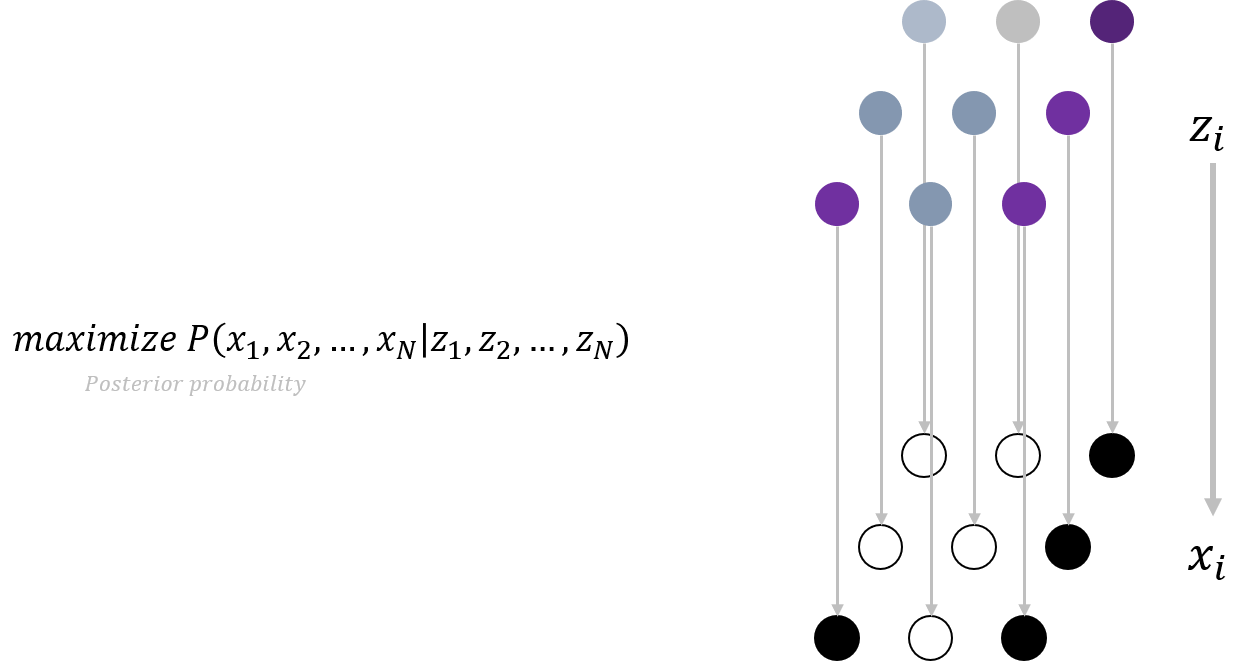
| Graph model에서는 주어진 \(Z\) 벡터에 대해 \(P(x_1,x_2,…x_N | z_1,z_2,…z_N)\)을 최대로 하는 \(X\)를 찾는 것을 목표로 합니다. |
이를 Posterior probability라고 하는데, 이 확률값을 바로 얻는 것은 쉽지 않습니다. 따라서 수학적으로 식을 변형합니다.
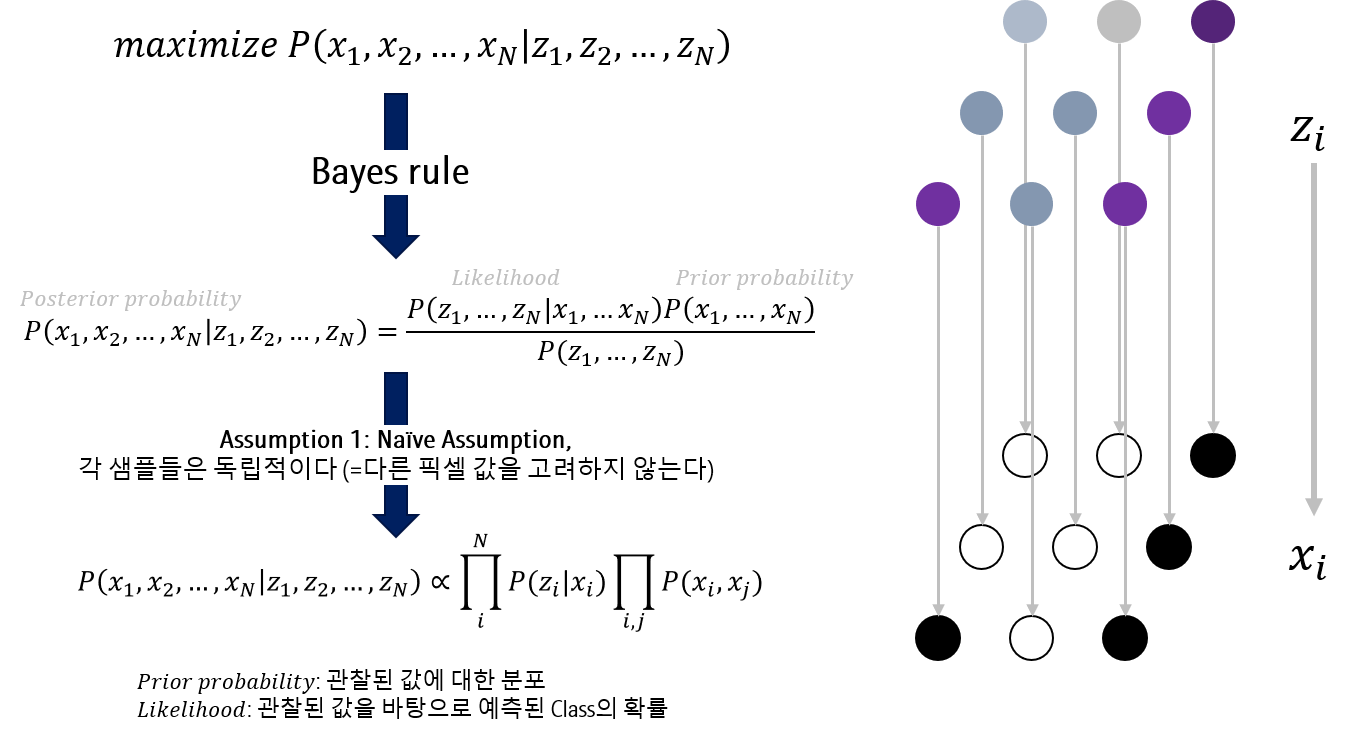
Posterior probability 수식을 Bayes rule로 풀어보면 아래와 같이 Likelihood \(P(z_1,…z_N \vert x_1,…z_N)P(x_1,…x_N)\)와 Prior probability \(P(x_1,…x_N)\)의 식으로 변형됩니다.
\[ P(x_1,x_2,…x_N \vert z_1,z_2,…z_N)=\frac{P(z_1,…z_N \vert x_1,…z_N)P(x_1,…x_N)}{P(z_1,…z_N)} \]
여기에 문제를 단순화하기 위해, 두 가지 Assumption을 갖습니다.
첫번째로 각 샘플은 독립적이라는 Naive assumption을 가정합니다. 각 샘플이 독립이라는 말은, 다시 말하면, \(x_i\)를 계산할 때, 다른 픽셀값들을 고려하지 않는다는 말이 됩니다.
Posterior probability는 아래와 같이 표현됩니다.
\[ P(x_1,x_2,…x_N \vert z_1,z_2,…z_N) \propto \prod_i^N P(z_i \vert x_i) \prod_{i,j}P(x_i, x_j) \]
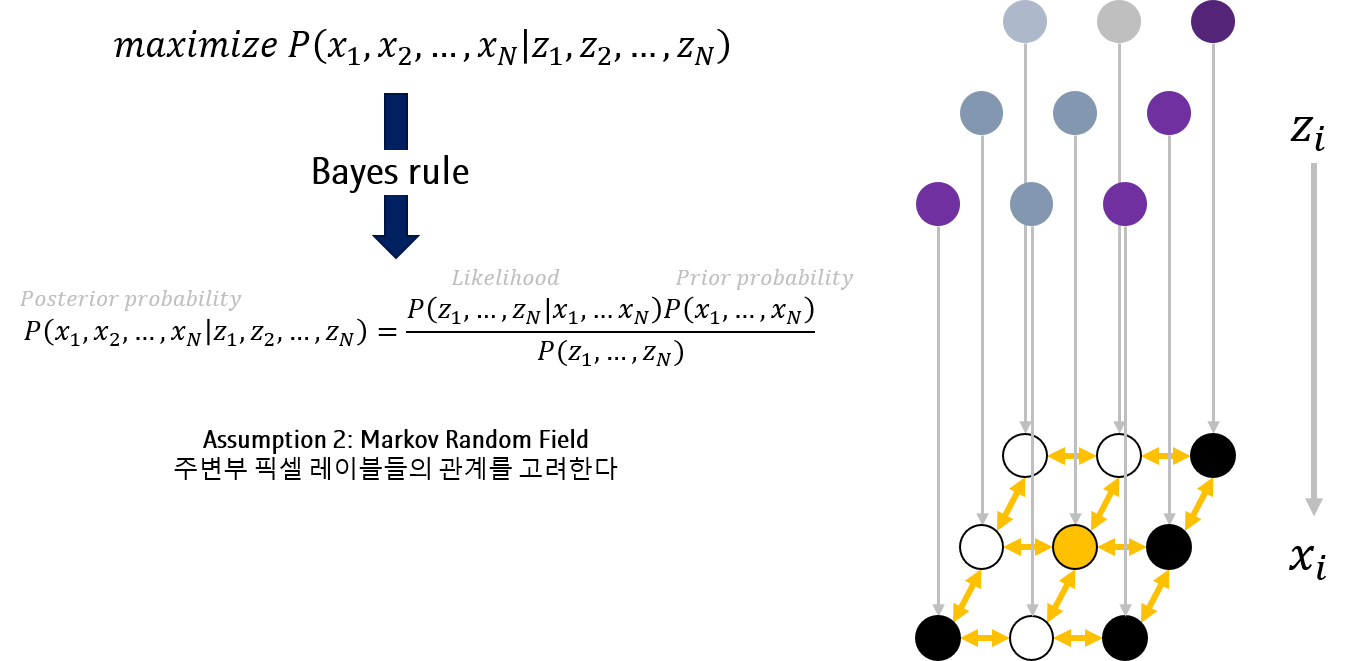
두번째 Assumption은 Markov Random FIeld입니다. 다른 픽셀값을 고려하지 않되, 주변에 위치한 픽셀의 label \(x_j\)는 고려합니다.
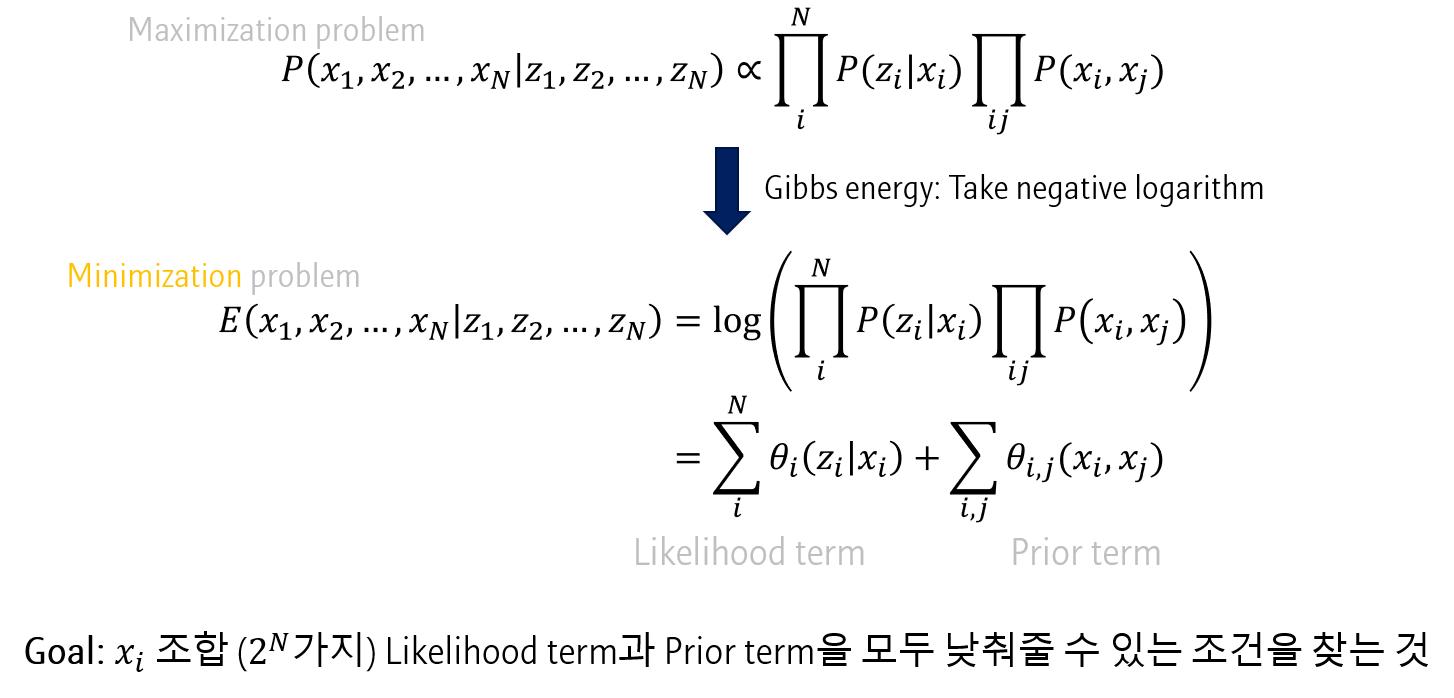
Posterior probability 를 최대화시키는 문제는 Negative logarithm을 적용한 Energy를 최소화하는 문제로 생각할 수 있습니다. (저는 이 부분을 아직 완전히 이해하지 못 했습니다)
따라서 아래와 같이 식이 변형됩니다.
\begin{aligned}
E(x1,x_2,…x_N \vert z_1,z_2,…z_N) &= log( \prod_i^N P(z_i \vert x_i) \prod{i,j}P(xi, x_j) ) \\
&=\sum_i^N \theta_i(z_i \vert x_i) + \sum{i,j} \theta_{i,j}(x_i,x_j)
\end{aligned}
위 식에서 \(\sumi^N \theta_i(z_i \vert x_i)\)은 Likelihood term으로, \(\sum{i,j} \theta_{i,j}(x_i,x_j)\)은 Prior term으로 생각할 수 있습니다.
위 식을 해석해보면, Assumption 1 (다른 픽셀값을 고려하지 않는다)에 따라 \(z_i\)와 \(x_i\) 사이의 관계만 보되 (Likelihood), Assumption 2 (주변부 픽셀의 label 값은 고려한다)에 따라 \(x_j\)는 고려하는 것으로 볼 수 있습니다 (Prior)
즉, Graph model에서 posterior probability 를 최대화하는 문제는 pixel-wise label \(x_i\) 의 \(2^N\)가지 모든 조합 중 likelihood term과 prior term을 모두 최소화하는 조건을 찾는 문제입니다.
lambda
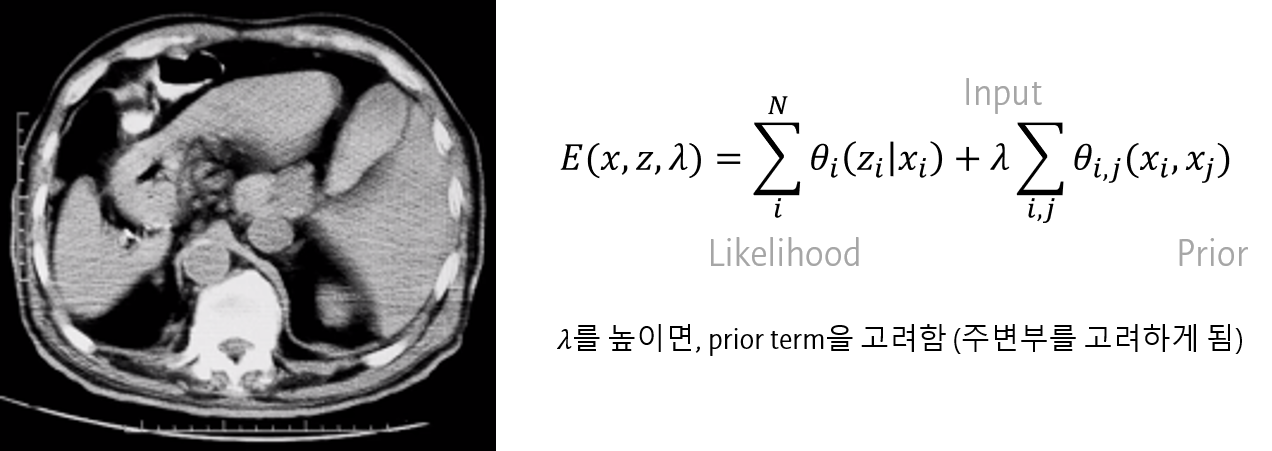
여기에 Prior term에 얼마나 가중치를 줄 지 나타내는 \(\lambda\)를 붙여 사용합니다.
알고리즘의 \(\lambda\)가 커지면, prior term에 대한 가중치가 높아집니다. 즉, 주변부 픽셀 label의 영향을 더 많이 받게 됩니다.
max-flow min-cut algorithm
max-flow min-cut 알고리즘은 좀 더 공부가 필요합니다. 대략적인 과정만 참고하세요
Graph model과 관련된 (?) 알고리즘 중 하나로 Max-flow min-cut (Mfmc) 알고리즘이 있습니다.
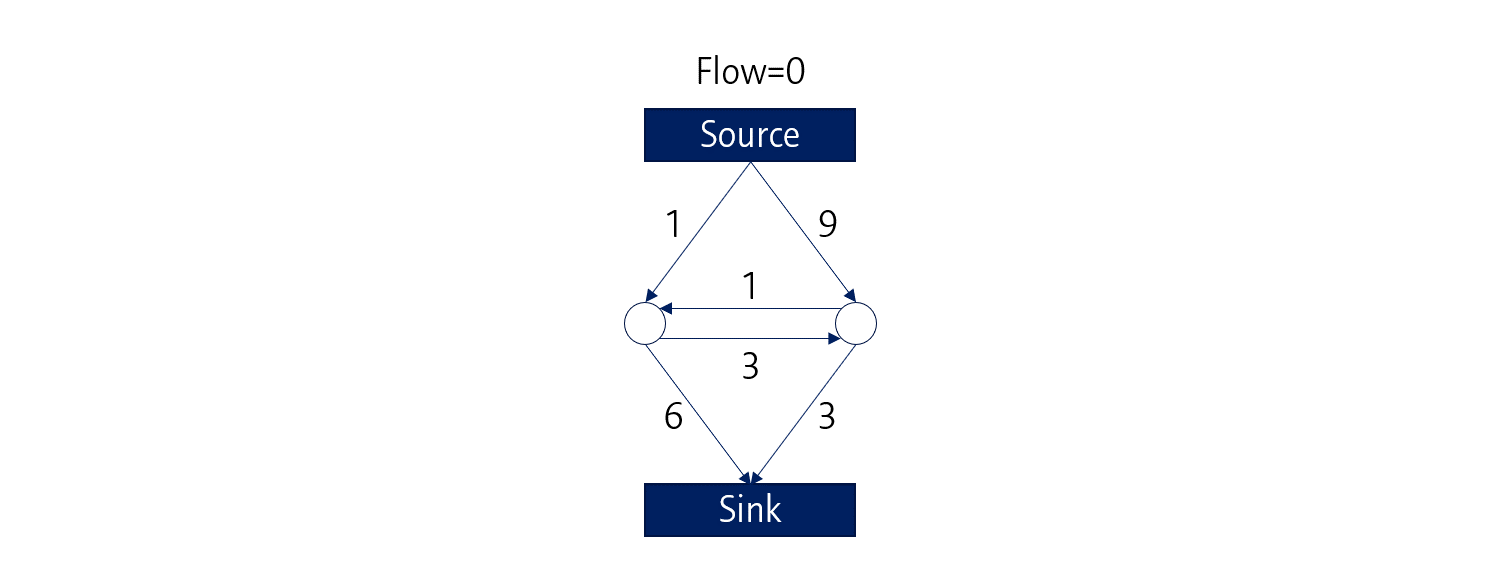
Mfmc 알고리즘에서는 Observation (Source)으로부터 Sink까지 가는 path들이 있고, 각 path들에는 capatcity가 존재합니다.
Source로부터 Sink까지 낮은 Capacity를 채워가며 가상의 물이 흐르고, 이 물에 의해 공간이 나뉜다고 생각하면 됩니다.
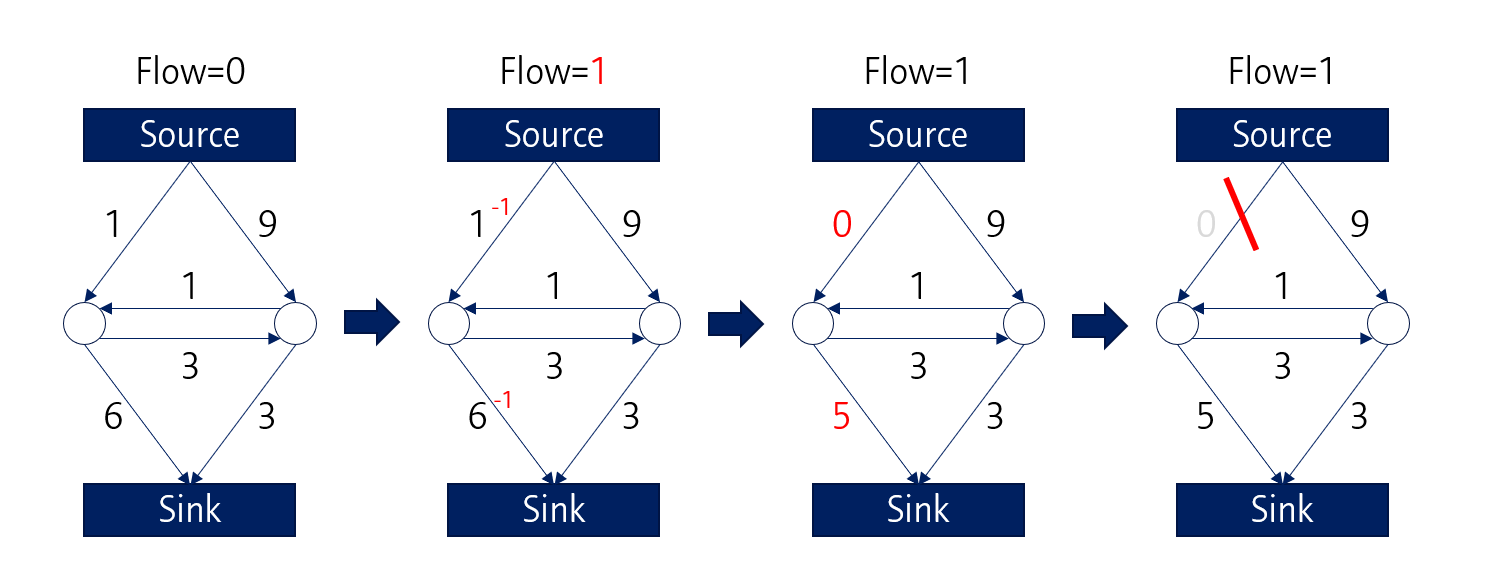
가장 먼저 좌측의 1, 6 path를 따라 Sink로 물이 흐르고, 해당 path들의 capacity는 1만큼 감소합니다. 좌상단의 1 path는 0으로 바뀌게 되므로, 이 path는 끊기게 됩니다.
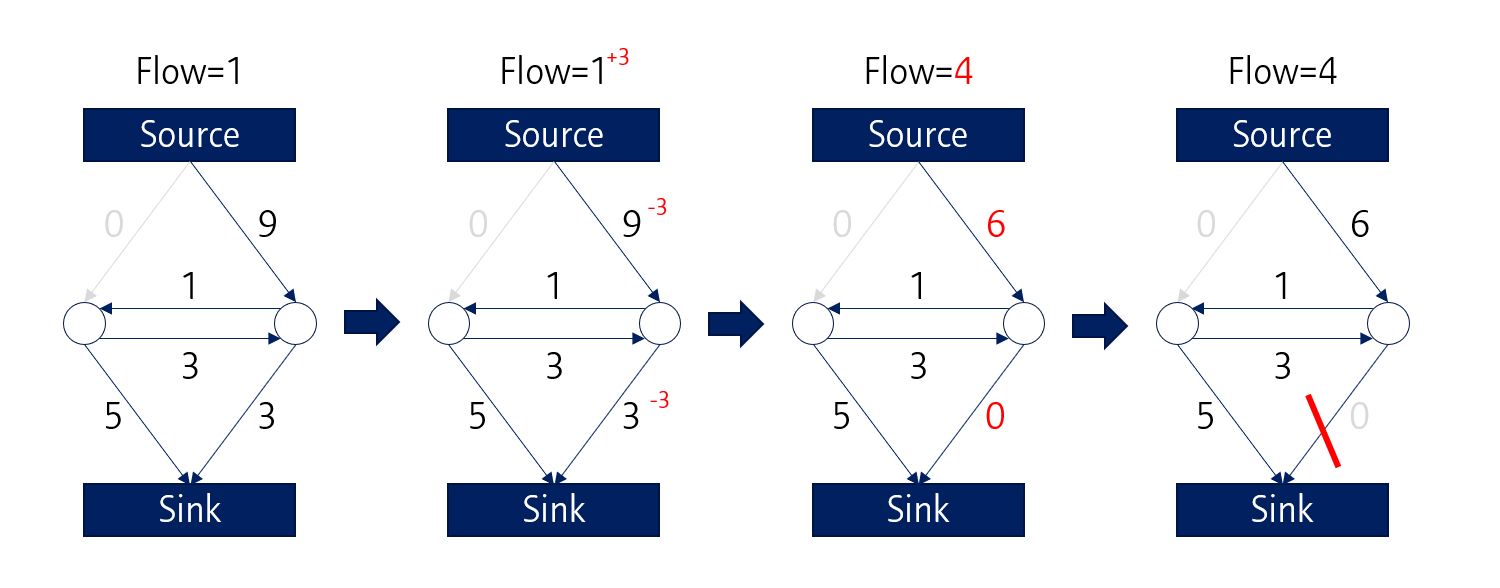
마찬가지로 이번에는 우측의 9, 3 path를 따라 물이 흐르게 되고, 해당 path는 capacity가 감소합니다. 그 결과, 우 하단의 3 path는 0이 되어 해당 path도 끊깁니다.
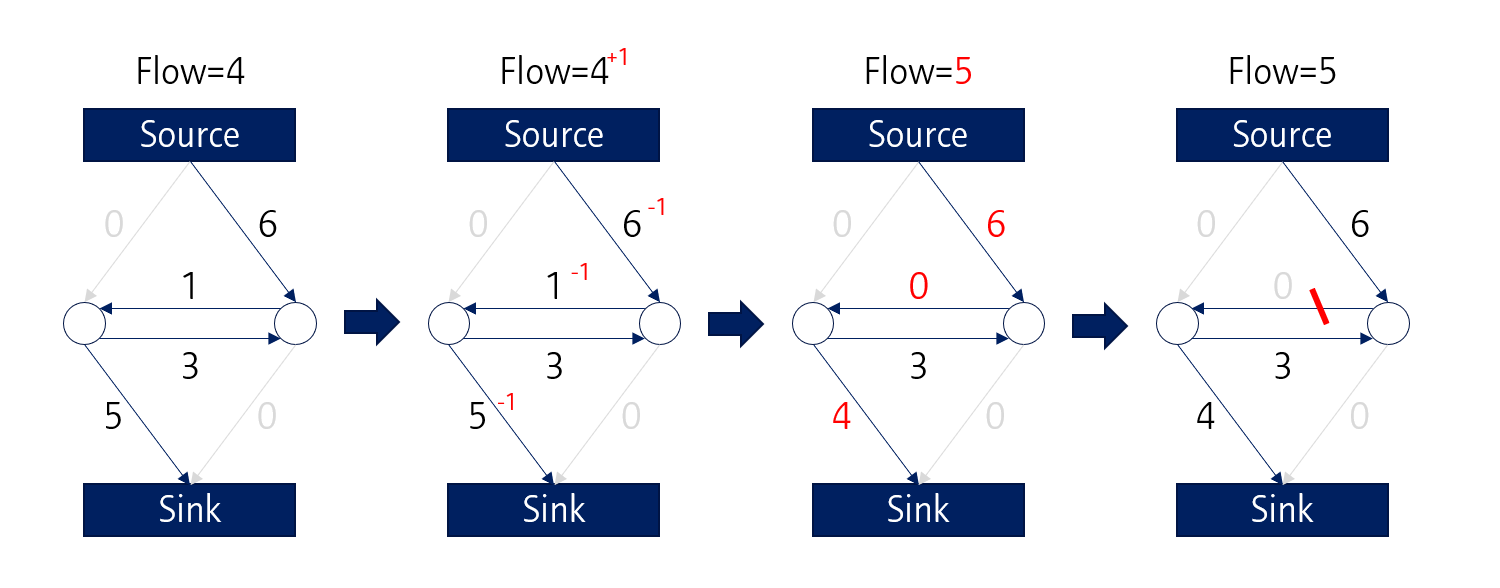
같은 방식으로 가운데 위치한 1 path도 끊기게 되면
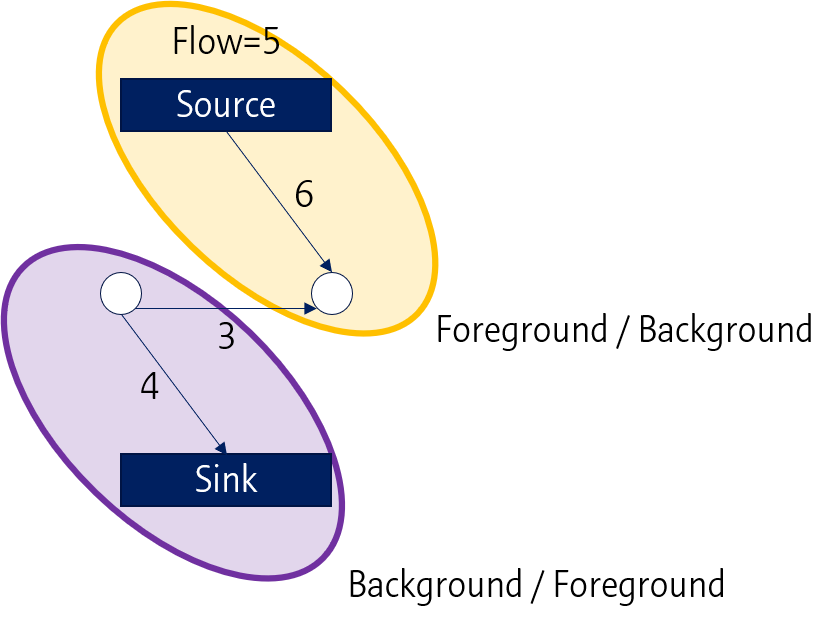
원래의 Graph는 두 개로 분리가 됩니다. 즉, Foreground/Background로 segmentation 되는 것으로 볼 수 있습니다.
Graph model이 익숙하지 않아서 이번 차시 강의의 내용은 전부 이해하지 못했습니다. 추후 시간이 허락하면 좀 더 공부해서 보완하고자 합니다.
다음 포스팅에서는 Active contour model을 정리해보고자 합니다

Leave a comment