부스팅 앙상블 (Boosting Ensemble) 2-2: Gradient Boosting for Classification

이전 글 보기: 부스팅 앙상블 (Boosting Ensemble) 2-1: Gradient Boosting for Regression

이전 포스팅에서는 Gradient Boosting 알고리즘 중 Regression 알고리즘을 정리했습니다.
이번 포스팅에서는 Gradient Boosting for Classfication 알고리즘을 정리해보고자 합니다.

Gradient Boosting for Regression과 마찬가지로, StatQuest라는 유투버의 Gradient Boost Part 3: Classification과 Gradient Boost Part 4: Classification Details를 참고했습니다.

Gradient Boosting for Classification

Gradient Boosting for Classification은 Gradient Boosting for Regression과 전체적인 흐름 (pseudo-residual을 계산하고 이를 예측하는 decision tree를 만들어나가는 과정)은 비슷하지만, 확률-log(Odds) 변환 같이 세부적인 내용에서 차이가 있습니다.

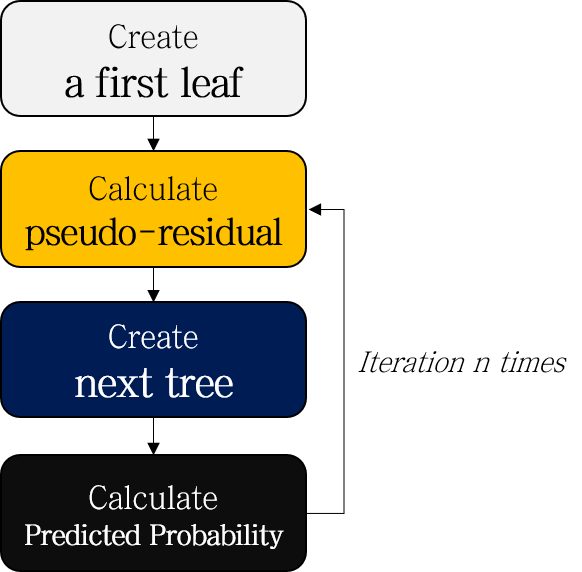
1. Create a first leaf
2. Calculate pseudo-residuals of probability
3. Create a next tree to predict pseudo-residuals
4. Calculate predicted probability
5. Repeat 2-4

• (Test) Scale, add up the results of each tree, and convert to probability

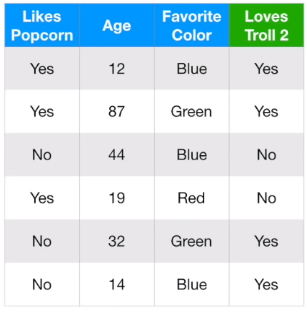
위 예시 데이터를 바탕으로 Gradient Boosting for Classification 과정을 정리해봅시다. 몇 가지 지표를 바탕으로 Troll 2를 좋아할지 예측하는 데이터입니다.

1. Create a first leaf

기억하세요, first leaf의 초기 prediction 값은 \(log(odds)\)를 사용합니다.

Odds는 임의의 사건 A가 발생하지 않을 확률 대비 일어날 확률의 비율입니다.

• 참고: Machine learning: Odds와 Log(Odds)

\[ odds=\frac{P(A)}{P(A^C)}=\frac{P(A)}{1-P(A)} \]

Loves Troll 2 데이터를 보면 Yes가 4개, No가 2개 있습니다. 따라서 초기 leaf 값은 \(log(odds)=log\frac{4}{2}=0.6931=0.7\)이 됩니다.

Log(Odds) 값을 사용하는 가장 쉬운 방법은 확률 값으로 변환하는 것입니다. Leaf 모델의 predicted probability는 아래와 같이 계산됩니다.

\[ P(Loves\; Troll\; 2=Yes)=\frac{e^{log(odds)}}{1+e^{log(odds)}}=\frac{0.7}{1+0.7}=0.6667=0.7 \]

이 후 계산에서는 편의를 위해 소수점 한 자리로 반올림합니다.

2. Calculate Pseudo-residuals of probability

Probability의 Pseudo-residual (실제값 - 예측값)을 계산합니다.

2.1 Observed probability

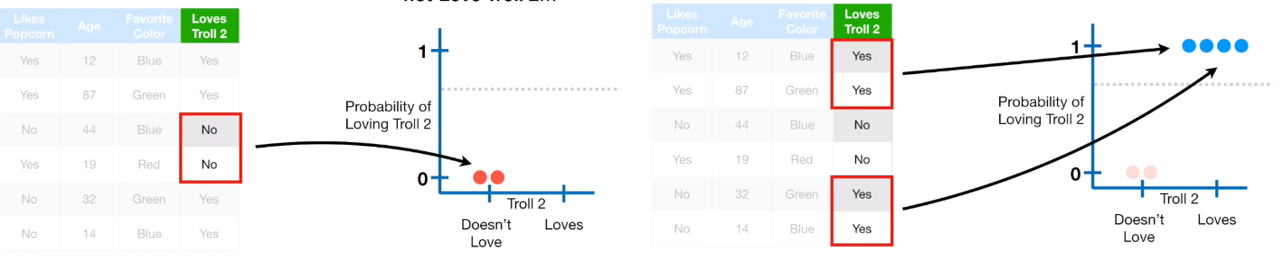
여기서 실제값 Observed probability는 Output의 Yes/No 값에 따라 1 또는 0의 값을 갖습니다.

2.2 Predicted probability

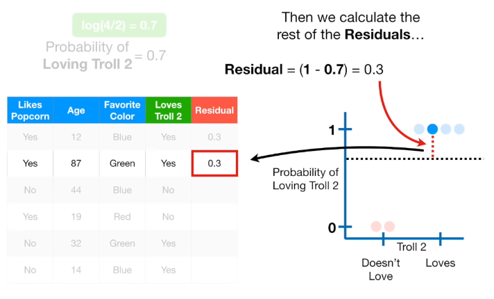
예측값으로는 이전 모델의 predicted probability을 사용합니다.
즉, 첫번째 트리를 만들 때는 first leaf의 predicted probability를 사용하므로 샘플마다 동일한 값을 사용하지만, 두 번째 트리부터는 샘플마다 다른 Predicted probability (Step 4에서 계산)를 사용하게 된다는 것을 기억해야 합니다.

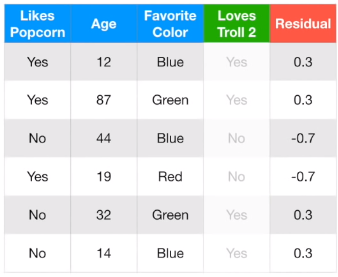
위와 같이 Pseudo residual 을 계산했습니다.

3. Create a next tree to predict pseudo-residual

3-1. Create a tree

이제 Pseudo-residual을 예측하는 decision tree를 만듭니다. 이 때 Gradient Boosting for Regression과 마찬가지로 maximum number of leaves로 제한을 줍니다. 예시에서는 3개로 제한을 주었지만, 실제로는 8~32값을 많이 사용한다고 합니다.

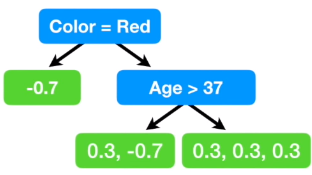
3-2. Calculate representative value by leaves

Gradient Boosting for Regression과 같이 한 leaf 는 동일한 prediction 값을 output 으로 내놓습니다. Regression에서는 단순히 pseudo-residuals의 평균값으로 대치했었는데, Classification에서는 조금 복잡합니다.

이는 First leaf 에서의 prediction 과 이후 tree model에서의 output 타입이 다르기 때문입니다.

First leaf의 prediction 값은 log(odds)입니다. 반면, decision tree에서의 pseudo-residual은 probability (실제값-예측값)으로 계산된 값입니다. 따라서 Gradient Boosting for Regression에서와 같이 두 종류의 값을 그대로 합치는 것이 불가능하고, 별도의 Transformation 과정이 필요합니다.

Gradient Boosting for Classification에서 주로 사용되는 방법 트리의 예측 probability 결과를 log(odds)로 변환하는 것입니다. 변환 식은 아래와 같습니다.

\[ \frac{\sum Residual_i}{\sum (Previous\; Probability_i \times (1-Previous\; Probability_i))} \]

위 변환을 통해 나온 값으로 각 leaf의 대표값을 지정해주면 됩니다.

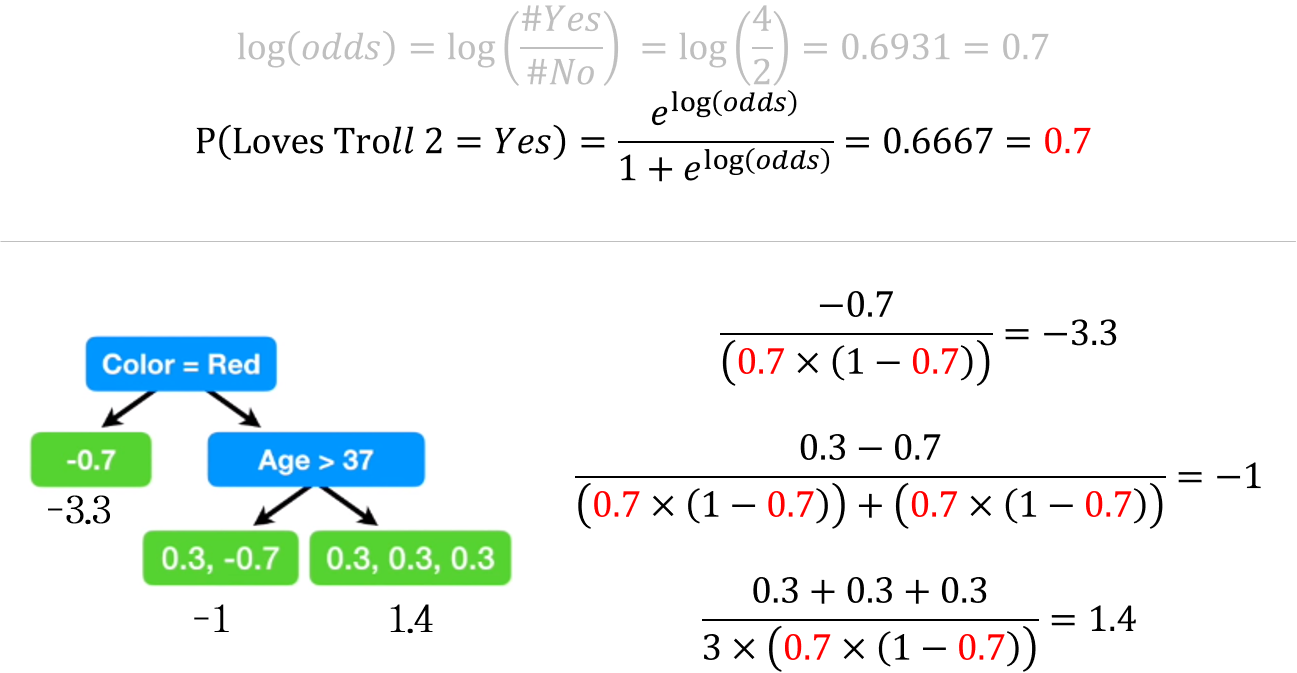
위와 같이 각 leaf의 representative value를 계산할 수 있습니다.

4. Calculate predicted probability

Pseudo-residual 계산에 사용될 샘플별 예측값을 계산해봅시다.

먼저 log(odds) 를 계산합니다. first leaf의 예측값과 tree의 예측값을 더해주면 됩니다. 이 때 tree의 예측값에 learning rate \(\eta\)를 곱해줍니다.

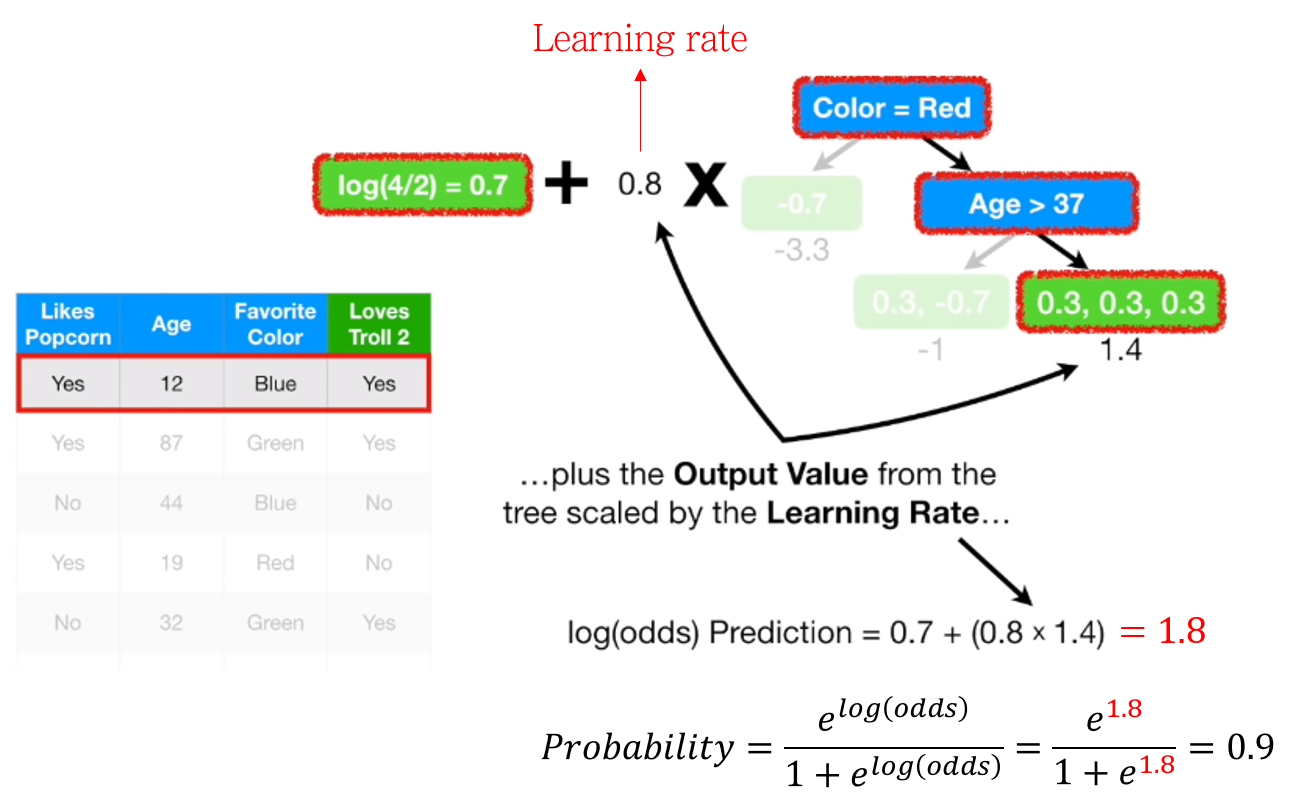
첫번째 샘플의 경우, 위와 같이 log(Odds)의 합으로 1.8을 얻었으며, 이를 확률로 변환하면 0.9의 값을 얻게 됩니다.

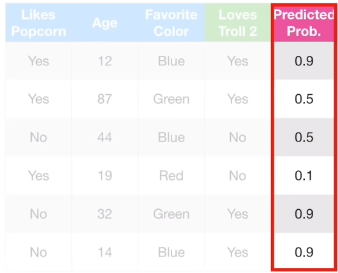
같은 방식으로 모든 샘플의 Predicted probability를 계산합니다.

5. Repeat 2-4

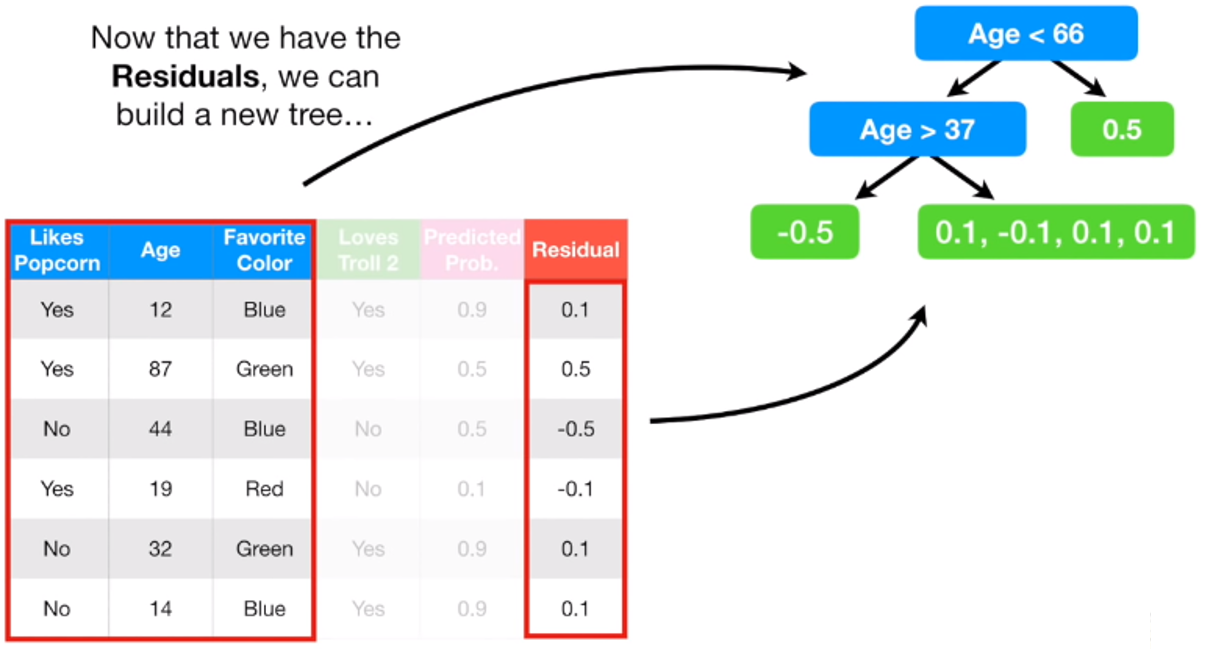
이제 Pseudo-residual을 계산할 준비가 끝났으니, Step 2부터 4를 반복해주면서 계속해서 새로운 트리를 만듭니다.

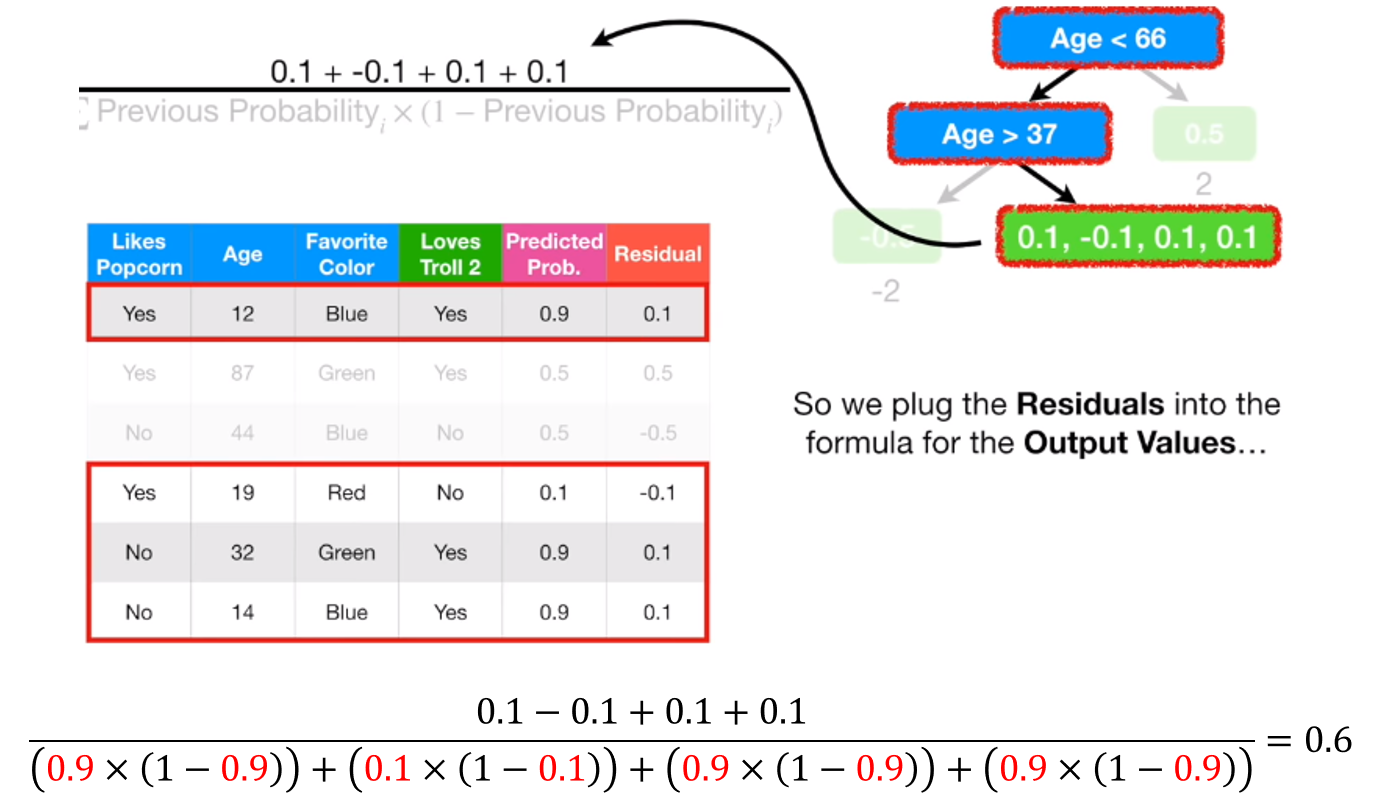
첫 번째 트리를 만들 때를 제외하고는 previous predicted probability가 샘플마다 다르다는 것을 꼭 기억하세요 !

(Test) Scale, add up the results of each tree, and convert to probability

최종적으로 first leaf와 tree들의 log(Odds)를 합해준 뒤, probability로 변환합니다.

이 확률값과 threshold (Binary classification 시 보통 0.5)와 비교하여 분류를 수행합니다.

---

이전 포스팅에서 Gradient Boosting의 Regression과 Classification 알고리즘의 공통되는 부분은 아래 내용으로 요약된다고 정리했습니다.

Create decision trees to predict residual (observed value – predicted value) of **__**, with limitation of maximum number of leaves.

빈 칸에, Regression에서는 Output value 그 자체, Classification은 Output class의 probability가 들어가면 말이 되겠네요.

Next: “Part 4 보고 관련 수식 이해하기”
다음 포스팅에서는 드디어 Kaggle에서 많이 사용되고 있는 대표적인 부스팅 앙상블 알고리즘인 XGBoost를 정리해보고자 합니다.

다음 글 보기: 부스팅 앙상블 (Boosting Ensemble) 3-1: XGBoost for Regression