Classification for MEDIA (7) Feature selection and extraction
이전 포스팅: Classification for MEDIA (6) Evaluation metrics for classification (분류모델 평가 지표)
이전 포스팅에서는 분류 모델을 평가하는데 사용되는 여러가지 지표 (Sensitivity, Specificity, Precision, AUROC, F1 score, accuracy)를 정리했습니다 이번 포스팅에서는 Classification 문제에 주로 사용되는 Feature selection, extraction 방법들을 정리해보고자 합니다.
Lasso (L1 regularization)
가장 먼저 L1 regularization, Lasso 를 이용한 Feature selection이 가능합니다. 별도의 포스팅으로 정리해두었습니다.
Mutual information
다음은 Mutual information 기반의 feature selection 입니다.
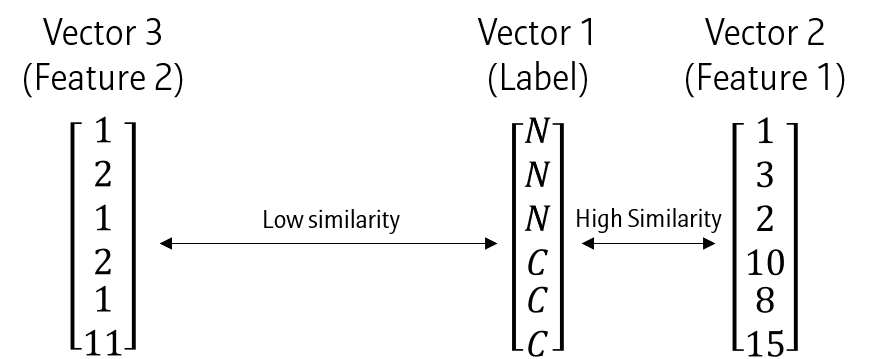
위와 같은 데이터가 있다고 할 때, Vector 1은 Vector 3보다는 Vector 2로 잘 표현할 수 있습니다. 즉, Vector 1-2에서 두 벡터간의 similarity가 더 높다고 할 수 있습니다. 이와 같이 데이터 간 Similarity를 측정하는 방법 중 하나가 Mutual information 입니다.
Entropy
Mutual information을 이해하기 위해 Entropy의 개념을 먼저 살펴봅시다.
사건들의 집합 중 사건 \(x\)가 일어날 비율을 확률 (Probability)라고 합니다. 확률은 \(p(x)\)라고 표기할 수 있습니다.
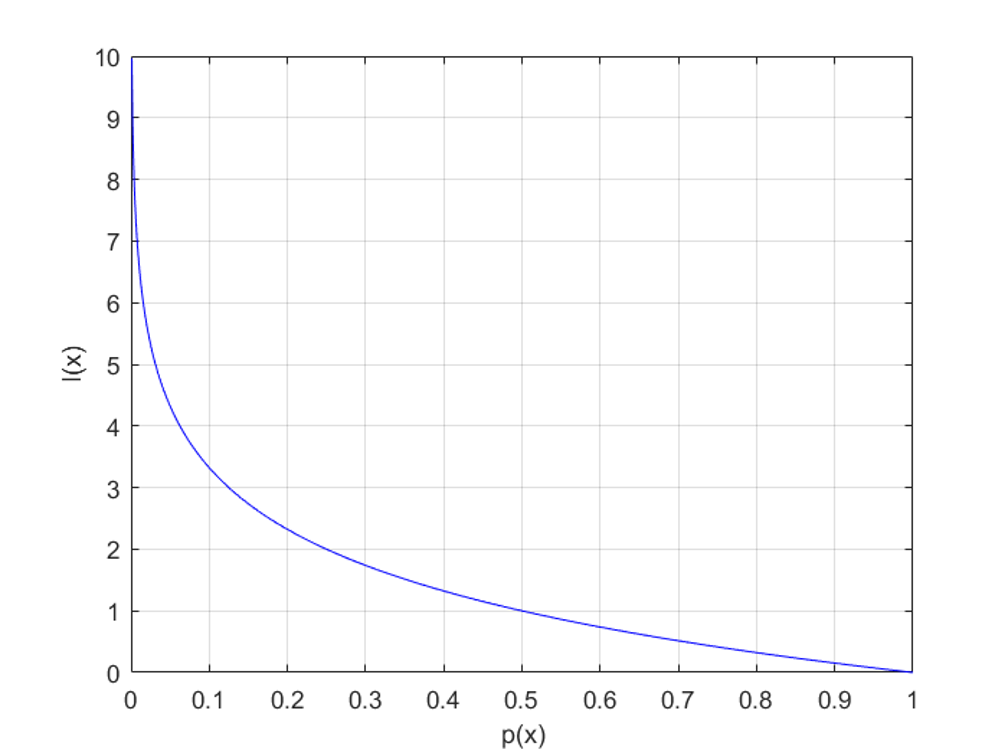
이 확률이 갖는 정보량 (Information)이라는 개념이 있는데, 이는 사건 \(x\)가 발생했을 때 놀라움의 정도로 해석할 수 있습니다. 따라서 위 그림과 같이, 확률이 낮을 수록 정보량이 높게 됩니다.
\[ I(x)=log \frac{1}{p(x)}=-log p(x) \]
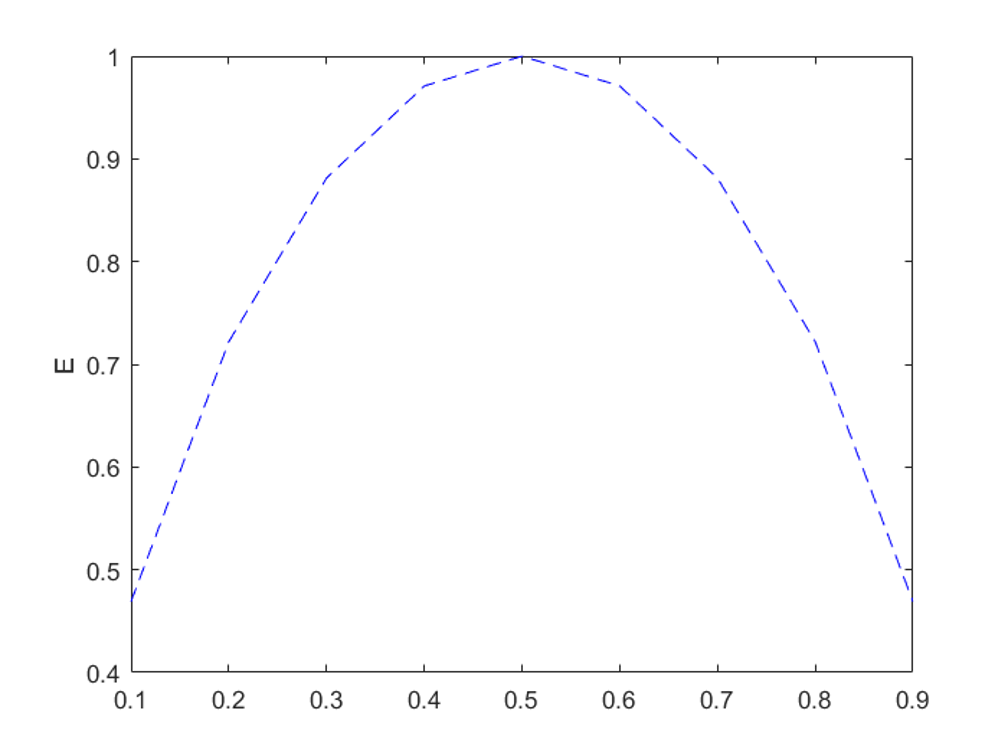
이제 Entropy가 나옵니다. 모든 사건들의 평균 정보량을 Entropy (무질서도)라고 하는데, 사건들의 확률값이 비슷할 때 커지는 특징을 갖습니다.
Joint entropy
두 사건 \(X\)와 \(Y\)의 관계를 Entropy로 나타낼 수 있습니다. 이를 Joint entropy \(H(X,Y)\)라고 하는데, 수식으로 나타내면 아래와 같습니다.
\[ Joint\; Entropy=H(X,Y)=-\sum_{i=1}^N \sum_{j=1}^M p(x_i, y_i)log p(x_i, y_i) \]
두 사건이 독립일 경우 (서로 관련이 없을 경우) Joint entropy는 각 사건의 Entropy의 합과 동일합니다.
\[ H(X,Y)=H(X) + H(Y) \]
이를 반대로 생각해보면, 두 사건이 서로 관련있을 경우에는 \(H(X)+H(Y)-H(X, Y)\)의 값으로 그 정도를 나타낼 수 있을 것입니다.
이를 Mutual information \(I(X;Y)\)라고 하며, 수식으로는 아래와 같습니다.
\begin{aligned}
I(X;Y)&=H(X)+H(Y)-H(X, Y) \\
&=\sum{i=1}^N \sum{j=1}^M p(x_i, y_i) log \frac{p(x_i, y_i)}{p(x_i)p(y_i)}
\end{aligned}
- Mutual information은 두 사건이 관련성이 없을 때 0의 값을 가지며, 관련 있을 때는 점차 커집니다.
Mutual information을 이용하는 알고리즘이 바로 Decision tree이며, Decision tree 및 여러 앙상블 기법에서는 각 feature와 class간 mutual information을 계산하여, feature별 중요도를 얻을 수 있습니다. 관련 내용은 이전 포스팅들을 참고해주세요.
mRMR
Mutual information을 이용한 또 다른 알고리즘은 minimum-Redundancy-Maximum-Relevance (mRMR)이라는 알고리즘입니다. 앞의 알고리즘과 다르게 feature-class 간 mutual information 뿐 아니라 feature-feature간 mutual information을 함께 사용해서 redundancy를 최소화시킵니다. 즉, 결과를 잘 설명하는 최적의 feature set를 찾되, 중복되는 feauture들은 고르지 않는 알고리즘입니다.
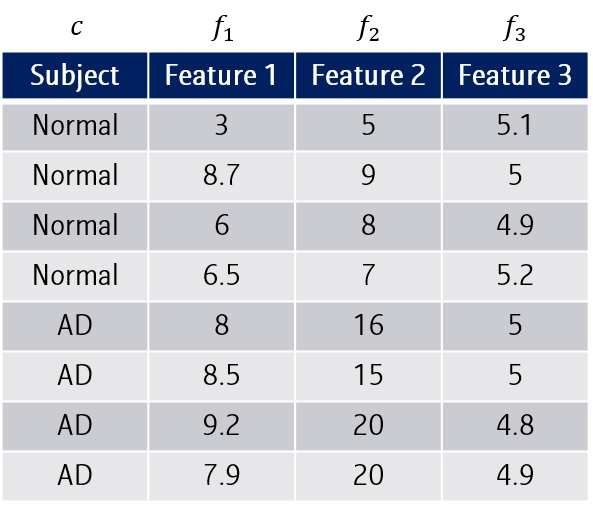
위와 같이 세 종류의 features \(f_1, f_2, f_3\)로 subject를 예측하고 있다고 해봅시다. 위에서 정리했듯, subject vector와 feature간 Mutual information \(D(S,c)\)은 최대화하되, 다른 feature들과의 mutual information \(R(S)\)은 최소화시키는 조합을 골라야겠죠.
이를 수식으로 나타내면 아래와 같습니다.
Class와 feature간 Mutual information
\[
D(S,c)=\frac{1}{|S|} \sum_{f_i \in S} I(f_i; c) \\
\]
feature와 다른 feature간 Mutual information
\[ R(S)=\frac{1}{S^2} \sum_{f_i, f_j \in S} I(f_1, f_2) \]
\(D(S,c\)를 최대화하는 동시에, \(R(S)\)를 최소화하는 feature set \(S\)를 찾는다.
\[ mRMR = \maxS [\frac{1}{|S|} \sum{fi \in S} I(f_i; c)-\frac{1}{S^2} \sum{f_i, f_j \in S} I(f_1, f_2)] \]
Auto-encoder
Autoencoder도 feature selection에 사용될 수 있습니다.
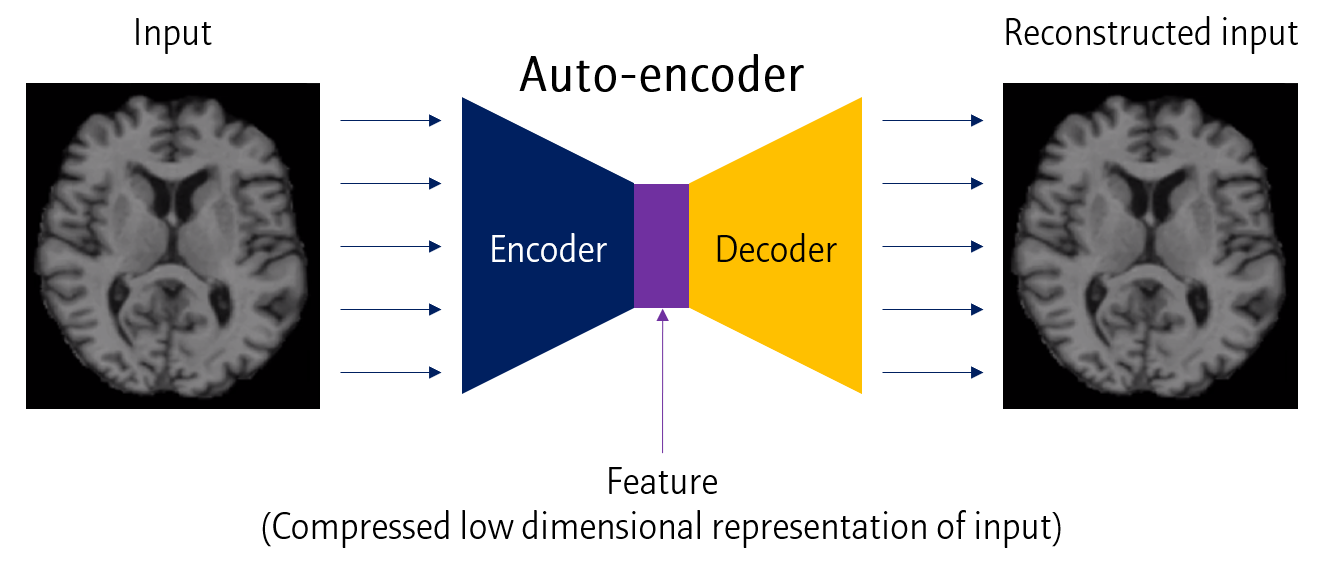
위와 같이 Input 데이터를 낮은 차원으로 압축한 뒤 (Encoder), 다시 원래 차원으로 변환시키는 (Decoder) 모델을 Auto-encoder라고 합니다.
이 때 낮은 차원의 데이터를 feature로 사용하는 개념입니다.
Class-Activation Map
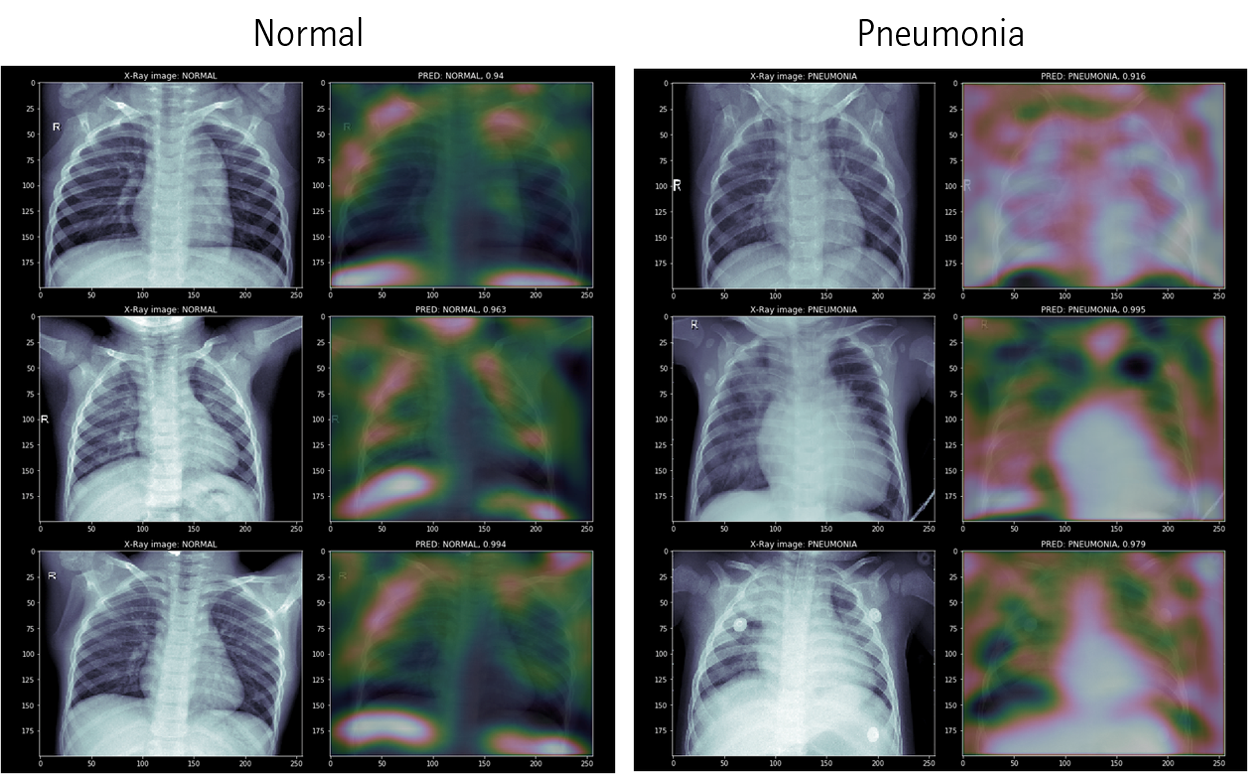
Class-Activation Map (CAM)은 feature selection이라기 보다는, feature visualization에 가깝습니다. CNN 모델에서 위와 같이 모델이 어느 부분을 보고 각 클래스라고 판정하는지 알려주는 알고리즘입니다. 별도의 포스팅에 CAM과 Grad-CAM을 정리해두었습니다.
Weakly supervised learninig
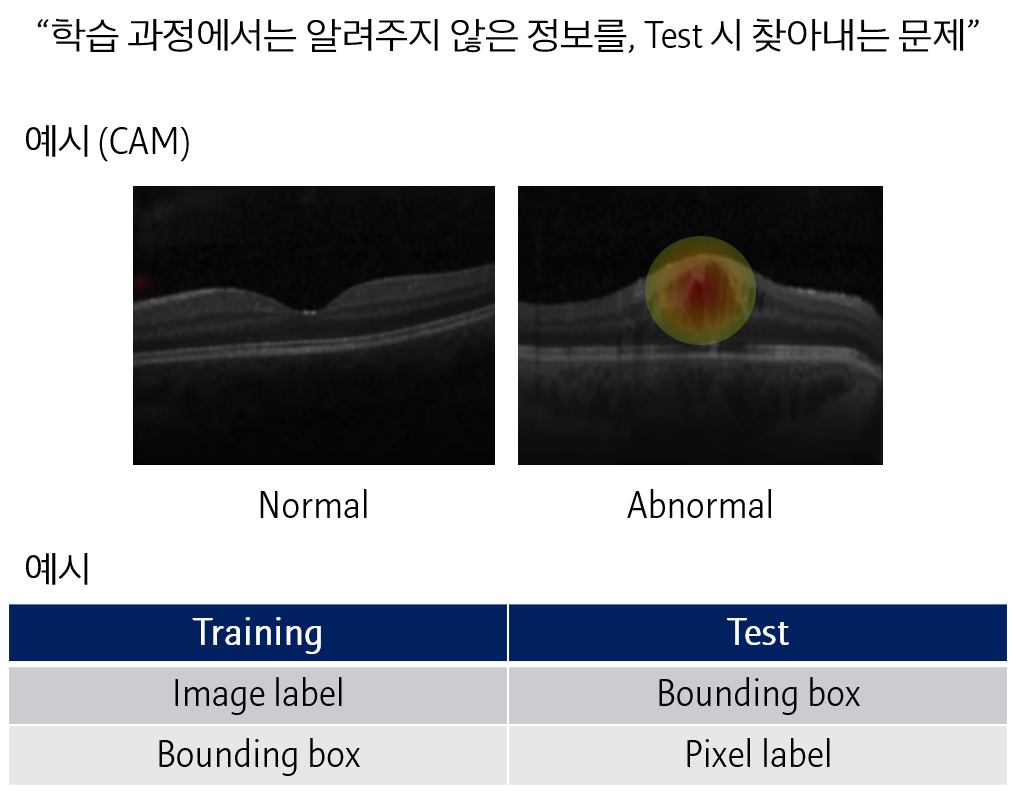
CAM은 이미지에 대한 결과를 분류하는 모델에서 각 모델이 이미지의 어느 부분을 살펴보고 있는지 알려주는 알고리즘이라고 정리했습니다. 이와 같이 모델을 학습시킨 정보보다, 알고자하는 정보가 더 디테일한 경우 이를 Weakly supervised learning이라고 합니다.
Image label을 예측하는 모델로부터 bounding box를 얻어내거나, Bounding box를 예측하는 모델로부터 pixel별 label을 얻어내는 문제를 말합니다.
Multiple instance learninng
Wakly supervised learning 에 대한 솔루션으로 Multiple instance learning이 있습니다.
모델에 대한 입력 데이터 (Instance)가 여러 개로 구성되어 있을 때, 입력데이터 중 일부 데이터에 따라 결과가 달라지는 경우가 있습니다.

위와 같이 열쇠꾸러미들이 있다고 할 때, Training 결과를 바탕으로 Test 열쇠꾸러미의 결과를 알 수 있을 것입니다.
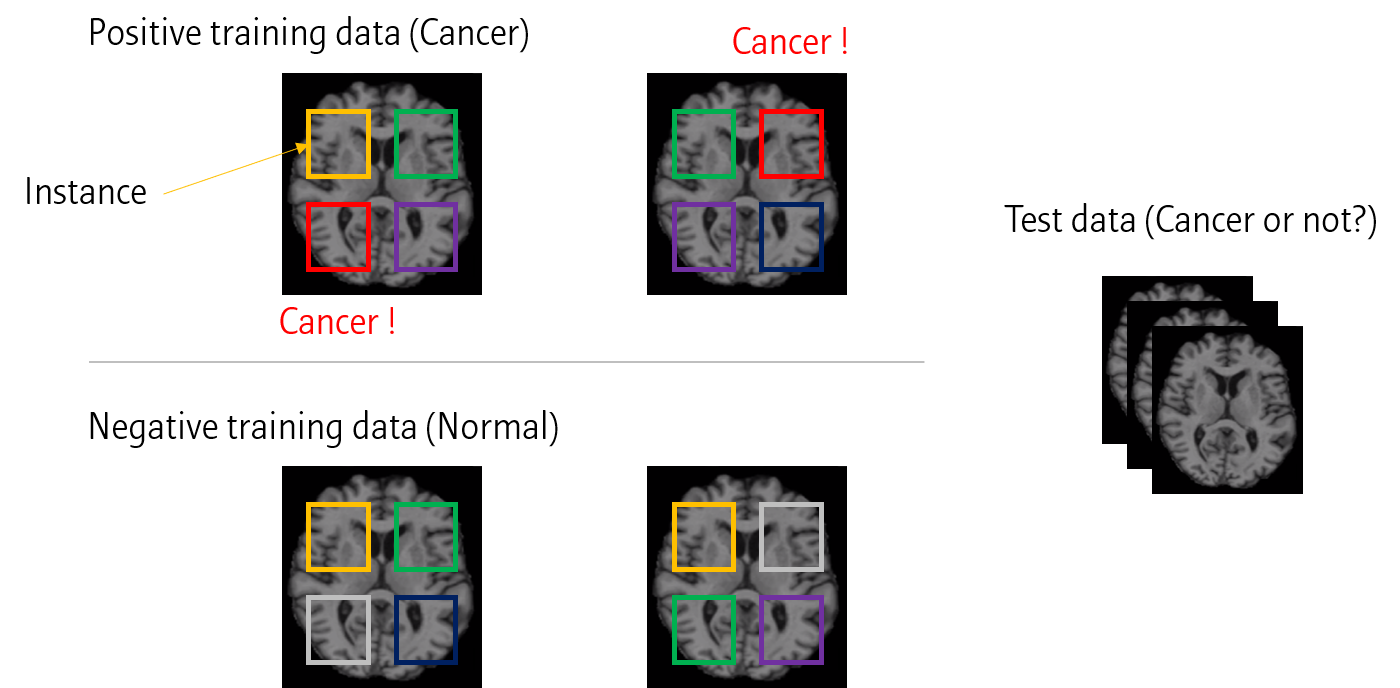
이를 의료영상에 적용하면 위와 같이 여러 이미지에서 작은 window를 통해 feature들을 추출해냅니다. 이후 이 feature 들로 모델을 학습시키면 (Cancer 이미지에서 나온 feature은 모두 cancer 데이터로 치기), 최종적으로 Test data에 대해서 pixel 별 label을 예측할 수 있습니다.
Multiple instance learninng은 좀 더 정리가 필요합니다
다음 포스팅부터는 Segmentation에 대해 정리해보고자 합니다

Leave a comment