의사결정 나무 (Decision Tree) ID3 알고리즘 설명
이전 글 보기: 의사결정 나무 (Decision Tree) 기본 설명
이전 글에 이어 의사결정 나무 (Decision Tree) 알고리즘을 설명하도록 하겠습니다.
본 포스팅에서 다룰 알고리즘은 의사결정 나무의 기본 알고리즘이라고 할 수 있는 ID3 알고리즘입니다.
ID3 알고리즘
ID3 알고리즘은 Iterative Dichotomiser 3의 약자입니다. Dichotomiser는 “이분하다”라는 뜻의 프랑스어로, 반복적으로 이분하는 알고리즘이라고 말할 수 있겠네요.
이전 포스팅에서 의사결정 나무의 분기는 불순도 (Impurity) 값이 작은 방향으로 이루어진다고 했습니다. ID3 알고리즘은 Impurity 값으로 엔트로피 (Entropy)를 사용합니다.
ID3의 Impurity: 엔트로피 (Entropy)
흔히 무질서도라고도 불리우는 엔트로피는 사건의 집합 \( S \)에 대한 불확실성의 양을 나타냅니다.
확률 (Probability)
사건 \( X_i \) 가 발생할 확률을 \( p(X_i) \) 로 정의합니다. \[ probability=p(x) \]
정보량 (Information)
이 때 이 사건 \( X_i \) 가 갖는 정보량 (Information)은 아래와 같이 계산됩니다. \[ information=I(x)=\log_2 \frac{1}{p(x)} \]
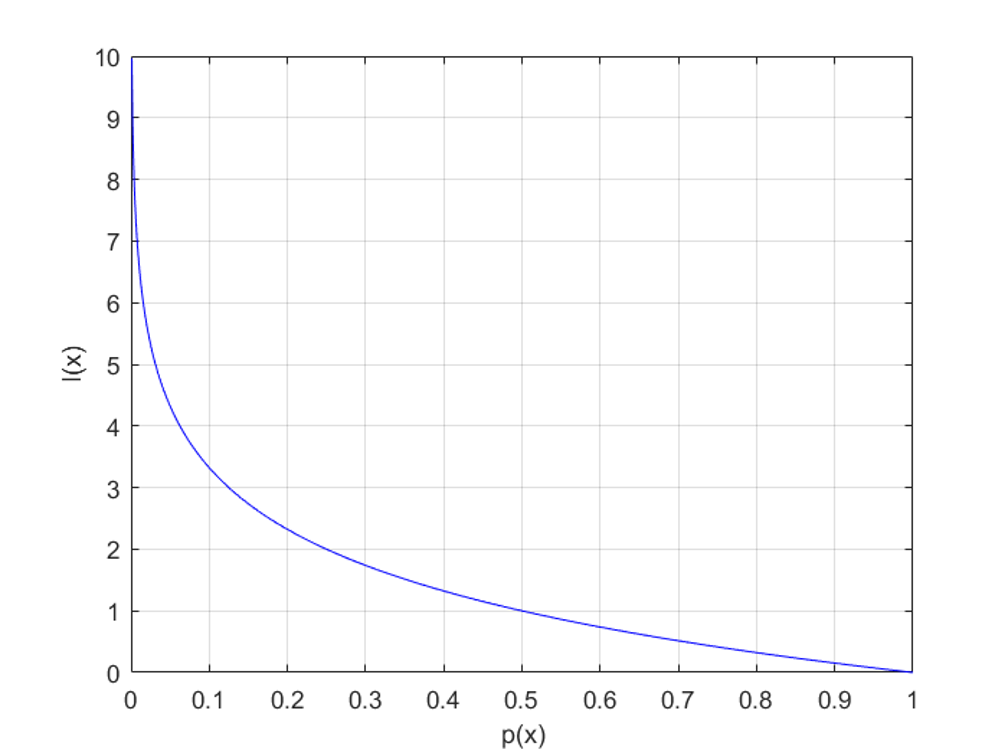정보량은 놀람의 정도라고 이해하면 쉬운데, 드물게 발생할 수록 더 많이 놀라는 경우 (예: 로또)를 생각하면 됩니다. 확률에 따른 정보량의 관계는 위 그림을 통해 확인할 수 있습니다.
엔트로피 (Entropy)
이어서 엔트로피는 아래 수식을 통해 계산할 수 있습니다. \[ Entropy=H(S)=\sum_{i=1}^c p_i\log_2 \frac{1}{p_i}=-\sum_{i=1}^c p_i\log_2 p_i \]
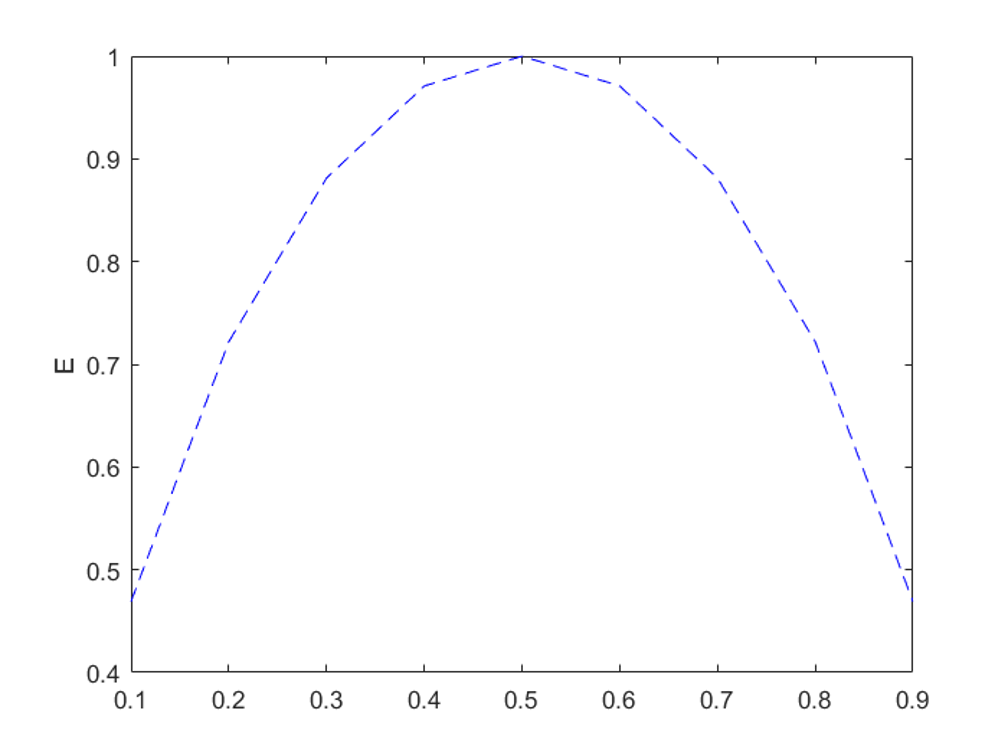이진 분류 (Binary classification) 문제에서 한 사건의 확률이 p(x)라고 할 때, 엔트로피는 위 그림과 같습니다.
Information Gain
ID3 알고리즘에서는 Entropy 값의 변화량을 나타내기 위해 Information Gain 이라는 개념을 사용했습니다.
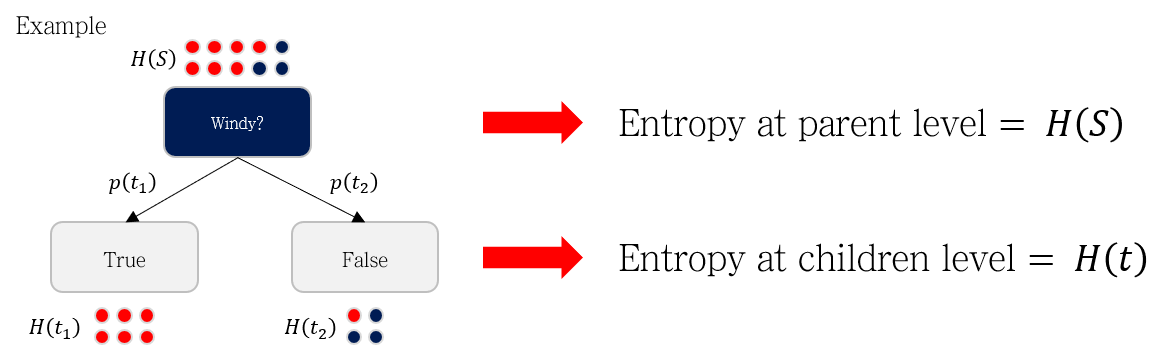위 그림에서 빨간 원은 Play=Yes를, 파란 공은 Play=No를 의미합니다. Windy 지표 (True OR False)를 이용해 데이터를 나눈다고 할 때, 분기 전후로 세 종류의 엔트로피를 계산할 수 있습니다.
- 분기 전 엔트로피 \( H(S) \)
- 분기 후 True에 해당하는 그룹의 엔트로피 \( H(S, True) \)
- 분기 후 False에 해당하는 그룹의 엔트로피 \( H(S, False) \)
Information Gain은 아래 수식과 같이 분기 전후 엔트로피의 차이값으로 계산됩니다. 이 때 분기 후 엔트로피는 양쪽 가지로 나뉘는 확률 \( p(t_i) \)를 가중치로 곱해 합쳐집니다.
\begin{aligned}
Information\; Gain&=IG(S,A)=H(S)-H(S,A) \\
&=H(S)-\sum p(t)H(t) \\
&=H(7,3)-(\frac{6}{10} \times 0+\frac{4}{10} \times 0.8113) \\
&=0.5568
\end{aligned}
최적의 Decision Tree를 만들기 위해, 여러 지표 중 분기 후 엔트로피 \(\sum p(t)H(t)\)가 작아지는 지표를 선택해야 합니다. 분기 전 엔트로피 \(H(S)\)는 동일하니, 이 말은 Information Gain이 가장 큰 지표를 선택하라는 말과 동일합니다.
ID3 알고리즘 예시로 이해하기
이전 포스팅에서 사용했던 예시로 ID3 알고리즘의 분기과정을 살펴봅시다.
| Outlook | Temperature | Humidity | Windy | Play |
|---|---|---|---|---|
| sunny | hot | high | FALSE | No |
| sunny | hot | high | TRUE | No |
| overcast | hot | high | FALSE | Yes |
| rain | mild | high | FALSE | Yes |
| rain | cool | normal | FALSE | Yes |
| rain | cool | normal | TRUE | No |
| overcast | cool | normal | TRUE | Yes |
| sunny | mild | high | FALSE | No |
| sunny | cool | normal | FALSE | Yes |
| rain | mild | normal | FALSE | Yes |
| sunny | mild | normal | TRUE | Yes |
| overcast | mild | high | TRUE | Yes |
| overcast | hot | normal | FALSE | Yes |
| rain | mild | high | TRUE | No |
Play를 예측하기 위한 변수로 Outlook, Temperature, Humidity, Windy 가 있습니다.
아무 분기가 일어나지 않은 상태의 엔트로피는 아래와 같이 계산됩니다.
\begin{aligned}
H(Play) &= -\sum_{i=1}^c p_i\log_2 p_i \\
&=-(\frac{5}{14}log_2\frac{5}{14}+\frac{9}{14}log_2\frac{9}{14}) \\
&=0.94
\end{aligned}
이제 각 지표별로 분기를 진행해봅시다.
-
Outlook
\begin{aligned}
H(Play,Outlook) &= p(sunny) \times H(3,2)+p(overcast) \times H(4,0)+p(rain) \times H(3,2) \\
&=\frac{5}{14}(-\frac{3}{5}log_2\frac{3}{5}-\frac{2}{5}log_2\frac{2}{5})+\frac{4}{14}(-\frac{4}{4}log_2\frac{4}{4}-\frac{0}{4}log_2\frac{0}{4})+\frac{5}{14}(-\frac{3}{5}log_2\frac{3}{5}-\frac{2}{5}log_2\frac{2}{5}) \\
&=0.6935 \end{aligned} -
Temperature
\begin{aligned}
H(Play,Temperature) &= p(hot) \times H(2,2)+p(mild) \times H(4,2)+p(cool) \times H(3,1) \\
&=\frac{4}{14}(-\frac{2}{4}log_2\frac{2}{4}-\frac{2}{4}log_2\frac{2}{4})+\frac{6}{14}(-\frac{4}{6}log_2\frac{4}{6}-\frac{2}{6}log_2\frac{2}{6})+\frac{4}{14}(-\frac{3}{4}log_2\frac{3}{4}-\frac{1}{4}log_2\frac{1}{4}) \\
&=0.2857+0.3935+0.2317 \\
&=0.911
\end{aligned}
- Humidity
\begin{aligned}
H(Play,Humidity) &= p(High) \times H(3,4)+p(Normal) \times H(6,1) \\
&=\frac{7}{14}(-\frac{3}{7}log_2\frac{3}{7}-\frac{4}{7}log_2\frac{4}{7})+\frac{7}{14}(-\frac{6}{7}log_2\frac{6}{7}-\frac{1}{7}log_2\frac{1}{7}) \\
&=0.7884
\end{aligned}
- Windy
\begin{aligned}
H(Play,Windy) &= p(True) \times H(3,3)+p(False) \times H(6,2) \\
&=\frac{6}{14}(-\frac{3}{6}log_2\frac{3}{6}-\frac{3}{6}log_2\frac{3}{6})+\frac{8}{14}(-\frac{6}{8}log_2\frac{6}{8}-\frac{2}{8}log_2\frac{2}{8}) \\
&=0.8921
\end{aligned}
각 지표 로 분기한 후 엔트로피를 계산했으니 각 경우의 Information Gain을 계산해봅시다.
- \( H(Play) – H(Play, Outlook) = 0.25 \)
- \( H(Play) – H(Play, Temperature) = 0.02 \)
- \( H(Play) – H(Play, Humidity) = 0.1514 \)
- \( H(Play) – H(Play, Windy) = 0.047 \)
Outlook으로 분기했을 때 Information Gain이 가장 크니 아래와 같이 첫 번째 level에서는 Outlook으로 분기합니다.
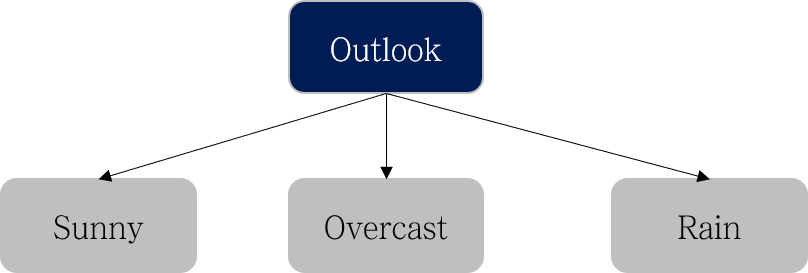
다음으로, 왼쪽의 Sunny 노드에 대해서 분기를 진행합니다. Sunny 노드의 데이터는 아래와 같습니다.
| Outlook | Temperature | Humidity | Windy | Play |
|---|---|---|---|---|
| sunny | hot | high | FALSE | No |
| sunny | hot | high | TRUE | No |
| sunny | mild | high | FALSE | No |
| sunny | cool | normal | FALSE | Yes |
| sunny | mild | normal | TRUE | Yes |
위 과정과 동일하게 Information Gain을 계산하면 다음 분기는 Humidity로 진행하면 된다는 것을 알 수 있습니다.
- \( H(Play) – H(Play, Temperature) = 0.571 \)
- \( H(Play) – H(Play, Humidity) = 0.971 \)
- \( H(Play) – H(Play, Windy) = 0.02 \)
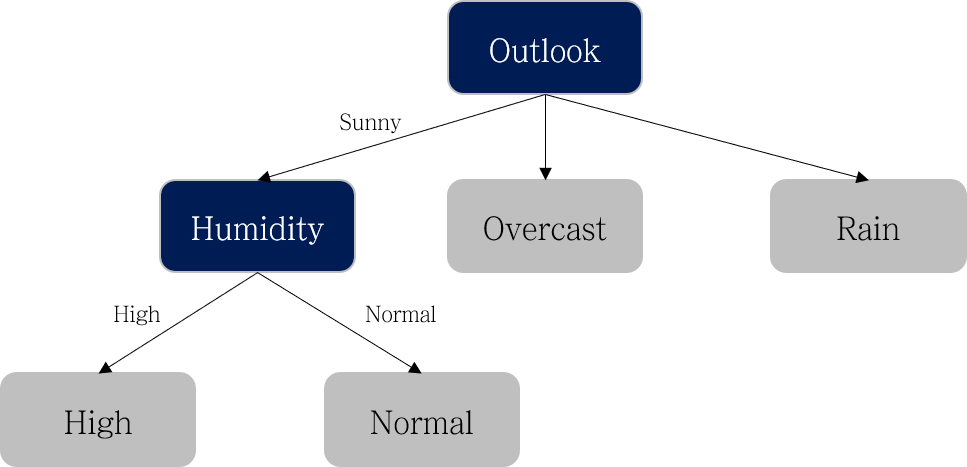
아래 표와 같이 Humidity에 따라 Play 데이터가 잘 나뉘는 것을 확인했으니 더 이상의 분기는 하지 않습니다.
정리하면 아래와 같이 되겠네요.
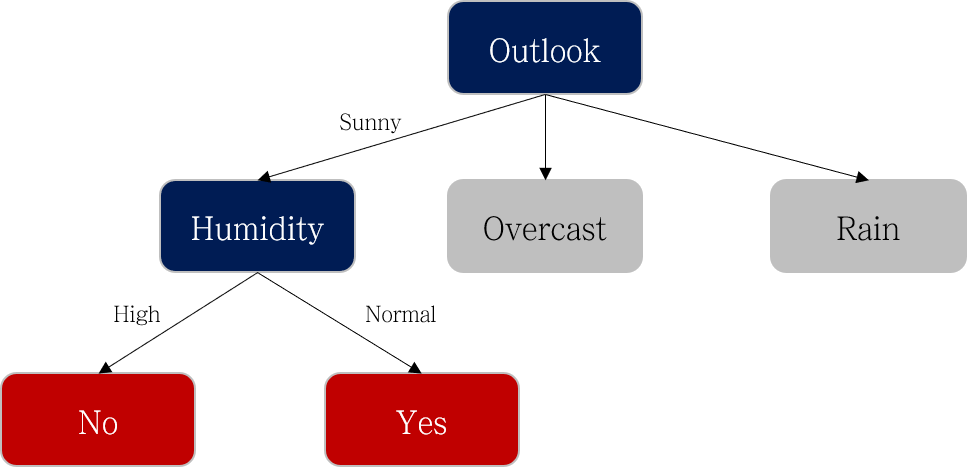
이 과정을 반복해서 수행해주면 아래와 같은 의사결정 나무가 완성됩니다.
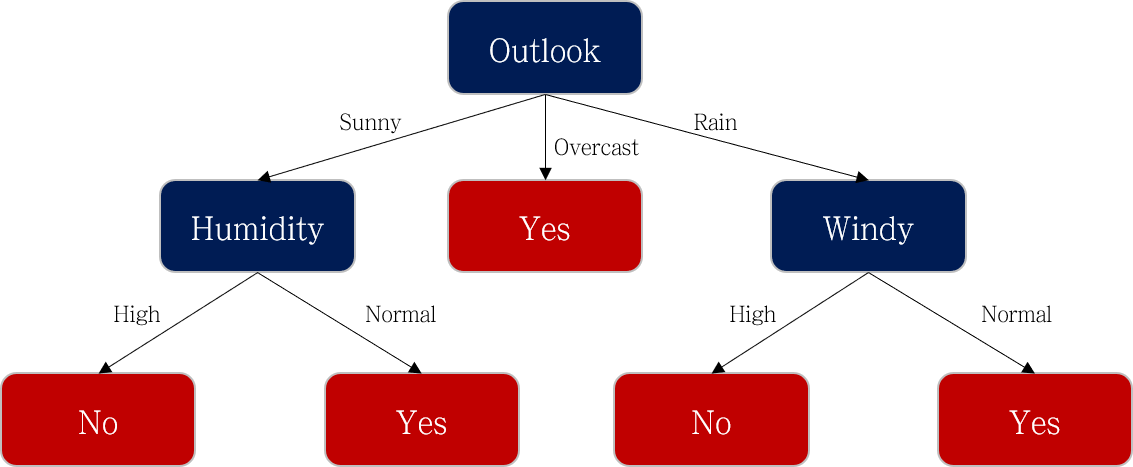
이번 포스팅에서는 ID3 알고리즘이 작동하는 원리를 예시를 통해서 이해해보았습니다. 다음 포스팅에서는 ID3보다 개선된 알고리즘인 C4.5 알고리즘을 공부해보도록 하겠습니다.
다음 글 보기: 의사결정 나무 (Decision Tree) C4.5 알고리즘 설명
Leave a comment