의사결정 나무 (Decision Tree) C4.5 알고리즘 설명
이전 글 보기: 의사결정 나무 (Decision Tree) ID3 알고리즘 설명
이전 포스팅에서는 의사결정 나무의 가장 기본적인 알고리즘인 ID3 알고리즘을 예시를 통해 정리했습니다.
이번 포스팅에서 소개할 C4.5 알고리즘은 ID3알고리즘과 동일하게 엔트로피를 불순도(Impurity)로 사용하는 알고리즘입니다.
C4.5 알고리즘
C4.5 알고리즘이 ID3알고리즘에 비해 개선된 점은 아래와 같이 요약할 수 있습니다.
- 정교한 불순도 지표 (Information gain ratio) 활용
- 범주형 변수 뿐 아니라 연속형 변수를 사용 가능
- 결측치가 포함된 데이터도 사용 가능
- 과적합을 방지하기 위한 가지치기
4가지 개선점이 어떻게 적용되었는지 하나씩 살펴보도록 하겠습니다.
개선점 1: 정교한 불순도 지표
ID3 알고리즘에서는 각 시점에서 모든 지표에 대한 분기 전후의 엔트로피를 기반으로 Information Gain (IG)을 계산하고, 이를 최대화하는 방향으로 지표를 결정했습니다.
하지만 이 알고리즘에는 한계점이 존재합니다.
Information Gain의 한계점
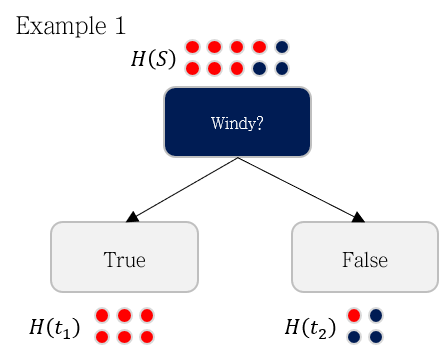
Windy라는 지표로 분기했을 때 데이터가 위와 같이 분기된다고 가정해봅시다. 이 경우의 Information Gain은 0.5568입니다.
\begin{aligned}
Information\; Gain&=H(7,3) - (\frac{6}{10}H(6,0)+\frac{4}{10}H(1,3)) \\
&=0.8813-(\frac{6}{10} \times 0+\frac{4}{10} \times 0.8113) \\
&=0.5568
\end{aligned}
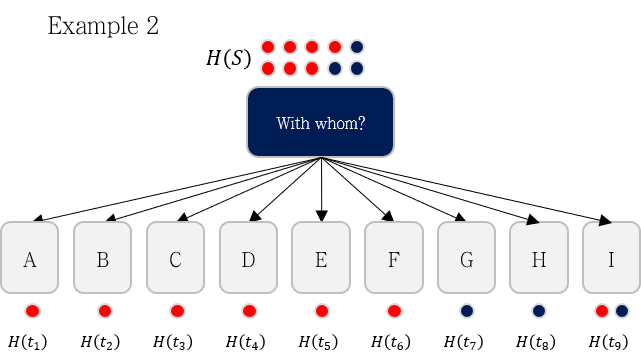
다른 지표인 With whom이라는 지표로 분기했을 때는 Information Gain이 0.6813이 나옵니다.
\begin{aligned}
Information\; Gain&=H(7,3) - (\frac{1}{10}H(1,0)+\frac{1}{10}H(1,0)+…+\frac{1}{10}H(0,1)+\frac{2}{10}H(1,1)) \\
&=0.8813-(\frac{1}{10} \times 0+…+\frac{2}{10} \times 1) \\
&=0.6813
\end{aligned}
두 경우를 비교했을 때, With whom 지표가 더 효과적인 지표라고 말할 수 있을까요? With whom 지표는 데이터를 너무 잘게 분해하기 때문에 좋은 지표라고 볼 수 없습니다.
Information Gain Ratio (GR)
C4.5 알고리즘에서는 이와 같은 문제를 해결하기 위해, Information Gain Ratio라는 지표를 사용하였습니다.
\[ Information\; Gain\; Ratio = \frac{IG}{IV} \]
\(IG\)는 ID3 알고리즘에서의 Information Gain을 의미하며, \(IV\)는 Intrinsic Value를 의미합니다.
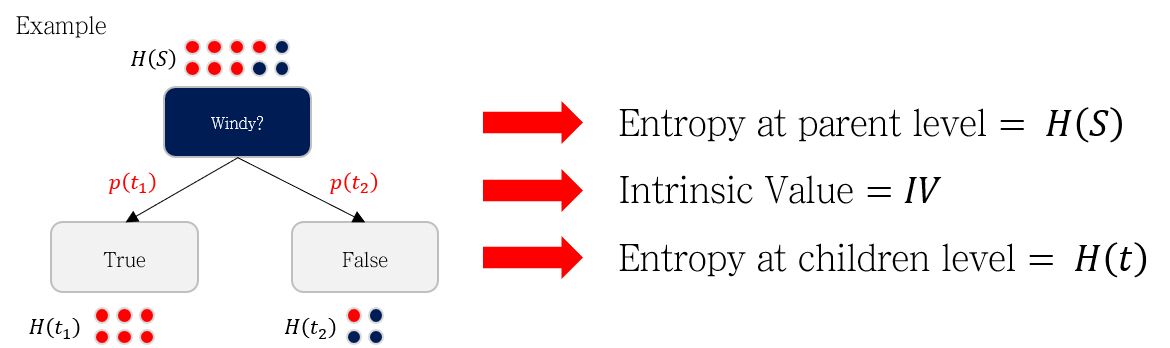
특정 지표로 분기했을 때 생성되는 가지의 수를 \(N\)이라고 하고, \(i\)번째 가지에 해당하는 확률을 \(p_i\)라고할 때, Intrinsic Value는 아래와 같습니다.
\[ Intrinsic\; Value=IV=-\sum_i^N p_i log_2 p_i \]
앞서 예시로 든 두 가지 지표 Windy, With whom에 대한 Information Gain Ratio를 계산하여 차이점을 비교해봅시다.

Windy 지표에 대한 Information Gain Ratio를 계산해보면, 첫 번째 경우는 0.5739라는 값을 얻을 수 있습니다.
\begin{aligned}
Information\; Gain\; Ratio&=IG/IV \\
&=\frac{0.5568}{-(\frac{6}{10}log_2 \frac{6}{10} + \frac{4}{10}log_2 \frac{4}{10})} \\
&=\frac{0.5568}{0.9701} \\
&=0.5739
\end{aligned}

동일한 방법으로 With whom에 대한 GR을 계산하면 0.2182라는 값을 얻습니다.
\begin{aligned}
Information\; Gain\; Ratio&=IG/IV \\
&=\frac{0.6813}{3.1219} \\
&=0.2182
\end{aligned}
아까와는 달리 Information Gain Ratio를 사용할 경우, Windy지표가 With whom 지표보다 더 좋은 지표임을 확인할 수 있습니다.
개선점 2: 연속형 변수를 사용 가능
C4.5 알고리즘에서의 두번째 개선점은 범주형 변수 (discrete variables)뿐 아니라 연속형 변수 (continuous variables)를 입력값으로 넣을 수 있다는 점입니다.
아래 테이블과 같은 데이터가 있다고 생각해봅시다. Temperature 변수는 연속형 변수입니다.
| Temperature | Play |
|---|---|
| 36 | No |
| 35 | No |
| 22 | Yes |
| 24 | Yes |
| 20 | Yes |
| 35 | No |
| 31 | Yes |
| 30 | No |
| 29 | Yes |
| 28 | Yes |
| 25 | Yes |
| 26 | Yes |
| 29 | Yes |
| 27 | No |
연속형 변수를 어떻게 나누면 될까요? 간단하게 생각해보면 특정 threshold 초과/이하의 값으로 나누면 되겠지요. 먼저 데이터를 변수값에 따라 정렬합니다. 그 후 Threshold 를 모든 breakpoints로 설정하면서 분기에 따른 불순도를 계산합니다. 이후 불순도를 최소화하는 지표를 선택하는 것처럼, 불순도를 최소화하는 threshold를 사용합니다.
그러면 여기서 breakpoints는 어떻게 정하게 될까요? 여기에는 아래 그림과 같이 크게 세가지 방법이 있습니다.
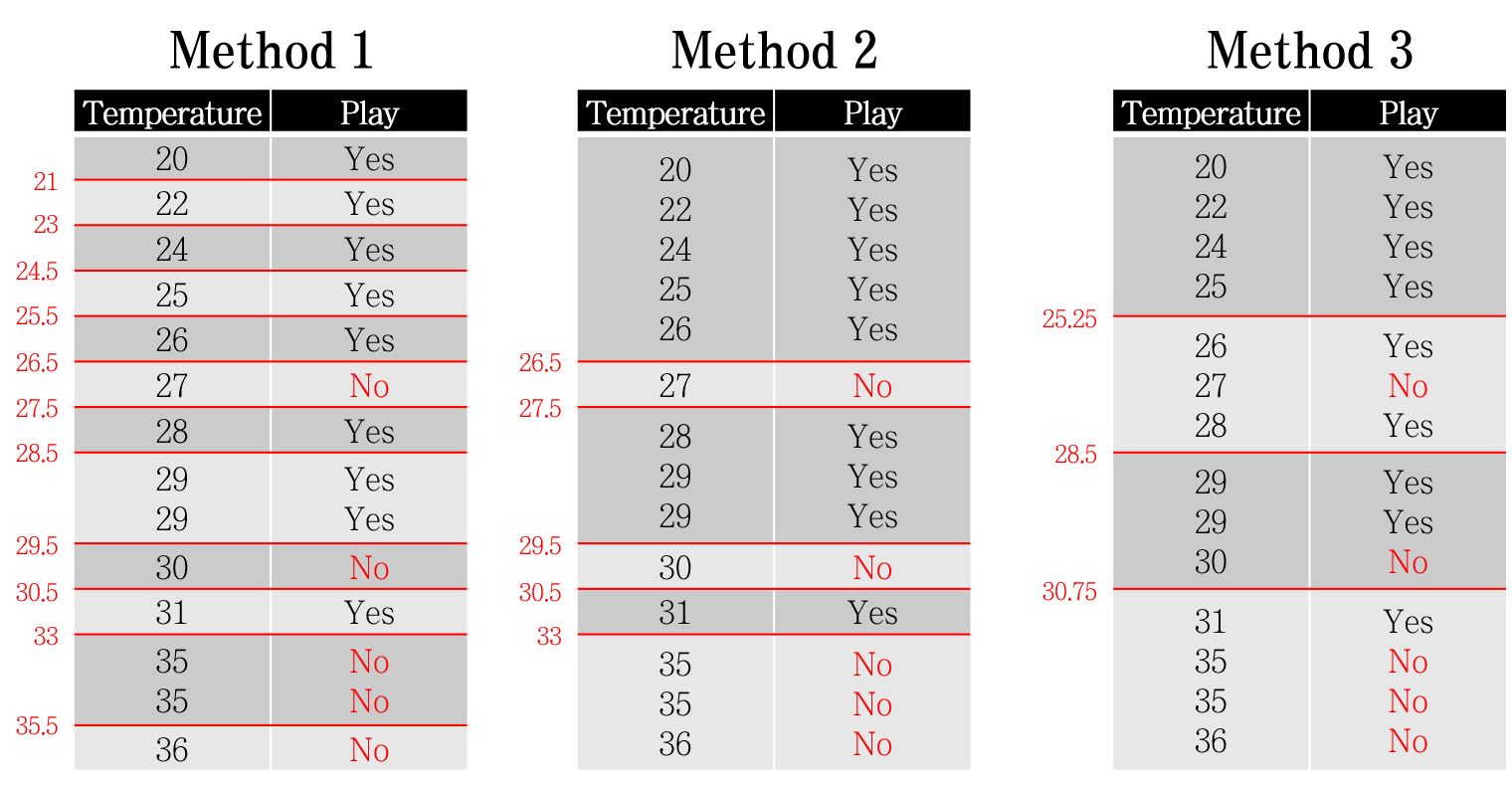
- 값이 바뀌는 모든 지점을 breakpoints 로 설정
- Output 클래스가 바뀔 때만 breakpoints로 설정
- Q1, Median, Q3 값을 breakpoints로 설정
이 중 방법 1을 예시로 Information Gain을 계산해보면 아래와 같습니다.
\[
IG(Play,Temperature(21))=0.04742 \\
IG(Play,Temperature(23))=0.1001 \\
IG(Play,Temperature(24.5))=0.1590 \\
IG(Play,Temperature(25.5))=0.2257 \\
IG(Play,Temperature(26.5))=0.3029 \\
IG(Play,Temperature(27.5))=0.09000 \\
IG(Play,Temperature(28.5))=0.1516 \\
IG(Play,Temperature(29.5))=0.3586 \\
IG(Play,Temperature(30.5))=0.1925 \\
IG(Play,Temperature(33))=0.4009 \\
IG(Play,Temperature(35.5))=0.2863
\]
이를 통해 Temperature 지표의 경우, 최적 threshold는 33도라는 것을 알 수 있습니다.
모든 지표 X 모든 breakpoints에 대해 Information Gain을 계산하여 비교한 뒤, 최적의 지표 X breakpoints 조합을 찾아 분기를 진행하면 됩니다.
개선점 3: 결측치가 포함된 데이터 사용 가능
C4.5 알고리즘의 세번째 개선점은 결측치가 포함된 데이터에도 사용이 가능하다는 것입니다.
아래와 같은 데이터가 있다고 생각해봅시다.
| Outlook | Play |
|---|---|
| Sunny | No |
| No | |
| Yes | |
| Rain | Yes |
| Rain | Yes |
| Rain | No |
| Overcast | Yes |
| No | |
| Yes | |
| Yes | |
| Yes | |
| Overcast | Yes |
| Overcast | Yes |
| Rain | No |
14개의 데이터 샘플 중 6개 샘플에 대해서는 Outlook 변수의 값이 결측치 (missing value)로 되어있는 상태입니다. 일반적으로는 이런 경우 분기 자체가 불가능하지만, C4.5 알고리즘에서는 이 문제를 Information Gain 을 계산하는 수식에 약간의 변화를 주어 해결했습니다.
핵심적인 내용을 요약하면 아래와 같습니다.
- 1단계: Entropy는 Non-missing value로만 계산
- 2단계: Information Gain는 Weighted Information Gain로 변경
-
\[ Weighted\; Information\; Gain=F \times IG(S,A)\\
F=proportion\; of\; non\; missing\; value \] - 3단계: Intrinsic Value는 missing value를 하나의 클래스로 보고 모든 데이터로 계산
예시
위 예시에 차례차례 적용을 해봅시다 !
- 1단계: Entropy는 Non-missing value로만 계산
\begin{aligned}
H(Play) &= -\sum_{i=1}^C p_i log_2 p_i \\
&=-(\frac{3}{8}log_2\frac{3}{8}+\frac{5}{8}log_2\frac{5}{8})
&=0.9544
\end{aligned}
\begin{aligned}
H(Play,Outlook) &= \sum p(t)H(t) \\
&= \frac{1}{8}H(1,0)+\frac{4}{8}H(2,2)+\frac{3}{8}H(0,3) \\
&= 0.5
\end{aligned}
\begin{aligned}
IG(Play,Outlook) &= H(Play)-H(Play,Outlook) \\
&= 0.4544
\end{aligned}
- 2단계: Information Gain는 Weighted Information Gain로 변경
\[ F=\frac{8}{14} \]
\begin{aligned}
Weighted\; Information\; Gain &= \frac{8}{14} \times 0.4544 \\
&=0.2597
\end{aligned}
- 3단계: Intrinsic Value는 missing value를 하나의 클래스로 보고 모든 데이터로 계산 총 4개의 클래스(sunny(n=1), rain(n=4), overcast(n=3), missing values(n=6))를 갖는 데이터셋으로 보고 Intrinsic Value를 계산합니다.
\begin{aligned}
IV &= -( \frac{1}{14}log_2 \frac{1}{14} + \frac{4}{14}log_2 \frac{4}{14} + \frac{3}{14}log_2 \frac{3}{14} + \frac{6}{14}log_2 \frac{6}{14} ) \\
&= 1.659
\end{aligned}
\begin{aligned}
Information\; Gain\; Ratio&=\frac{0.2597}{1.659} \\
&=0.1565
\end{aligned}
개선점 4: 과적합을 방지하기 위한 가지치기
의사결정 나무가 깊어질수록, training data에 대해서는 잘 분류하지만, 새로운 종류의 데이터 (test data)는 잘 분류하지 못하는 과적합 (overfitting) 문제가 발생하게 됩니다.
가지치기 (Pruning)
따라서 의사결정 나무가 너무 깊어지지 않도록 중간에 노드를 잘라주는 가지치기 (pruning) 과정이 필요합니다. 가지치기에는 사전 가지치기(pre-pruning)와 사후 가지치기(post-pruning) 과정이 있습니다.
- 사전 가지치기: 의사결정 나무를 완성하기 전에 가지치기를 수행합니다
- 사후 가지치기: 의사결정 나무를 완성한 후에 가지치기를 수행합니다.
이 중, C4.5 알고리즘에서는 사후 가지치기 알고리즘을 적용했습니다.
사후 가지치기 (Post-pruning)
-
Step 1: Data segmentation 사후 가지치기는 의사결정 나무가 완성된 후에 가지치기를 진행하는 방식입니다. 따라서 데이터를 training/test 데이터가 아니라 training/pruning/test 데이터로 나눕니다.
-
Step 2: Complete decision tree with training data Training data만으로 의사결정 나무를 만듭니다.
-
Step 3: Pruning with test data Pruning data로 가지치기를 수행합니다.
상위 노드부터 차례차례 \(e\)값을 계산합니다.
\begin{aligned}
e&=\frac{f+\frac{z^2}{2N}+z\sqrt{\frac{f}{N}-\frac{f^2}{N}+\frac{z^2}{4N^2}}}{1+\frac{z^2}{N}} \\
N&=sample\; size \\
f&=Error\; rate \\
z&=z\; score \; (default\; z=0.69)
\end{aligned}

자식노드들의 \(e\)값의 weighted sum 값과 부모노드의 \(e\) 값을 비교합니다. 만약 부모노드의 \(e\)값이 더 작다면, 해당 분기는 진행하지 않고 가지치기를 수행합니다.
- Step 4: Prediction with test data 완성된 pruned decision tree를 이용해 Test data 에 대한 결과를 예측합니다.
이번 포스팅에서는 C4.5 알고리즘의 특징들을 알아보았습니다.
다음 포스팅에서는 엔트로피 기반 불순도가 아닌 지니 계수를 불순도를 사용하는 CART (Classification And Regression Tree) 알고리즘에 대해 알아보도록 하겠습니다.
다음 글 보기: 의사결정 나무 (Decision Tree) CART 알고리즘 설명

Leave a comment