의사결정 나무 (Decision Tree) CART 알고리즘 설명
이전 글 보기: 의사결정 나무 (Decision Tree) C4.5 알고리즘 설명
이전 포스팅에서는 의사결정 나무에서 엔트로피를 불순도로 사용하는 ID3와 C4.5 알고리즘을 정리해보았습니다. 이번 포스팅에서는 엔트로피 외에 다른 불순도 지표를 사용하는 CART 알고리즘에 대해 정리해보도록 하겠습니다.
CART 알고리즘
CART는 ID3알고리즘과 비슷한 시기에, 별도로 개발된 알고리즘으로 Classification And Regression Tree의 약자입니다.
이름 그대로 Classification뿐 아니라 Regression도 가능한 알고리즘인데, 이 외에도 앞서 소개한 알고리즘들과 몇 가지 차이점이 존재합니다.
- 불순도: Gini index
- Binary tree
- Regression tree
위 세가지 항목에 대해 하나씩 살펴보도록 하겠습니다.
불순도: Gini index
Gini index는 엔트로피와 같은 불순도 (Impurity) 지표입니다. \(C\)개 사건의 집합 \(S\)에 대한 Gini index \(G(S)\)는 아래 수식으로 표현됩니다.
\begin{aligned}
G(S) &= \sum{i=1}^C p_i(1-p_i) \\
&= \sum{i=1}^C pi - \sum{i=1}^C pi^2 \\
&= 1 - \sum{i=1}^Cp_i^2 \\
\end{aligned}
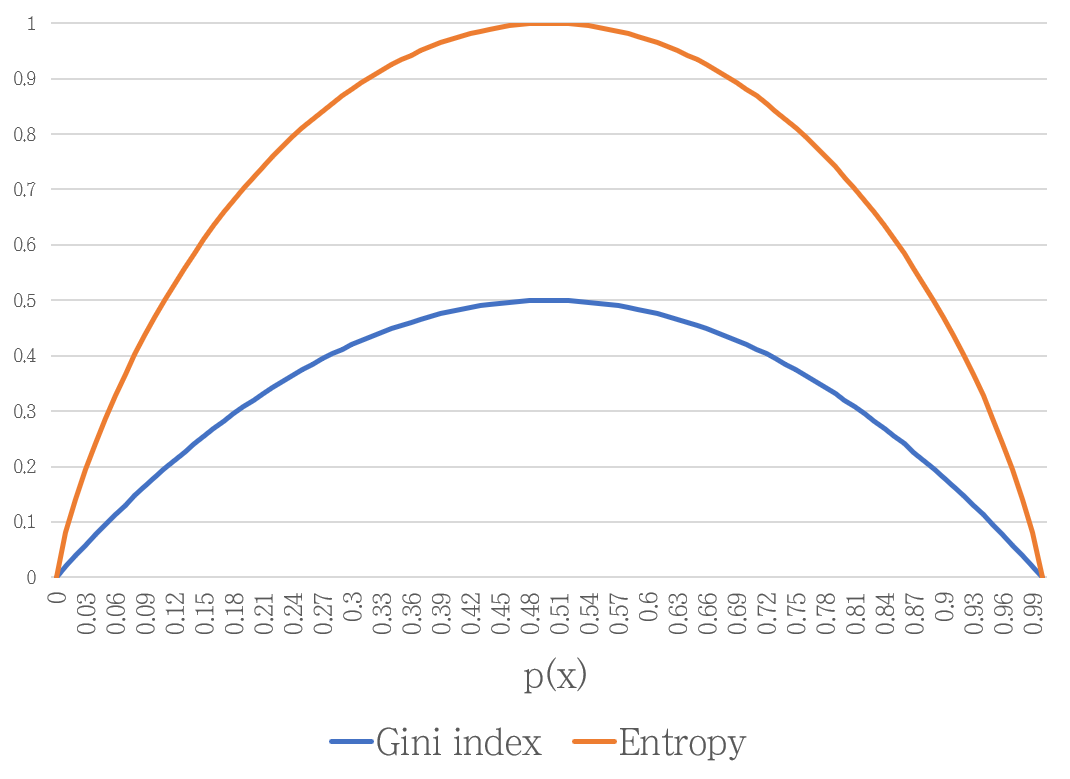
Gini index는 엔트로피와 같이 분류가 잘 될 때 낮은 값을 갖습니다. 따라서 CART 알고리즘에서는 모든 조합에 대해 Gini index를 계산한 후, Gini index가 가장 낮은 지표를 찾아 분기합니다.
ID3 알고리즘에서 Information Gain을 이용하는 것과 동일하기 때문에, 본 포스팅에서는 계산 과정은 생략하도록 하겠습니다.
Binary tree
CART 알고리즘의 또 하나의 특징으로는 가지 분기 시, 여러 개의 자식 노드가 아닌 단 두 개의 노드로 분기한다는 것 입니다 (Binary tree).
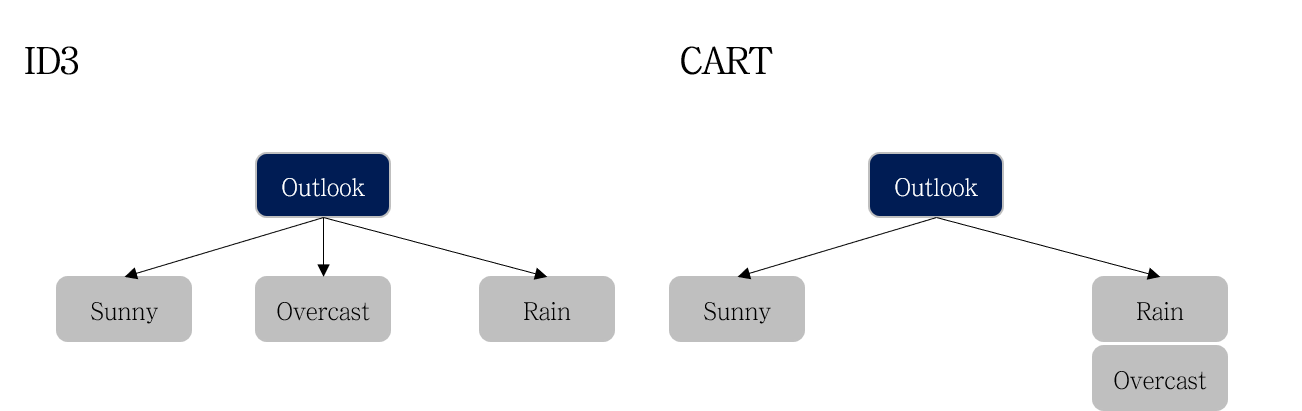
좌측은 ID3 알고리즘, 우측은 CART 알고리즘의 분기를 나타냅니다. ID3 의 경우 모든 클래스 (e.g., Sunny, Overcast, Rain) 로 가지가 뻗어져나갑니다. 따라서 ID3 알고리즘의 경우 지표별 Information Gain을 한 번씩만 계산하면 됩니다.
\[
IG(Play,Outlook) \\
IG(Play,Temeperature) \\
IG(Play,Humidity) \\
IG(Play,Windy)
\]
반면, CART는 ‘하나의 클래스와 나머지’와 같이 가지가 생성됩니다. 따라서 아래 예시와 같이 모든 지표 X 모든 클래스 개수만큼 비교가 필요합니다.
\[
IG(Play,Outlook=sunny) \\
IG(Play,Outlook=overcast) \\
IG(Play,Outlook=rain) \\
IG(Play,Temperature=hot) \\
IG(Play,Temperature=mild) \\
IG(Play,Temperature=cool) \\
IG(Play,Humidity=high) \\
IG(Play,Humidity=normal) \\
IG(Play,Windy=TRUE) \\
IG(Play,Windy=FALSE) \\
\]
Regression tree
Classification And Regression Tree 라는 이름답게, CART 알고리즘은 Regression(회귀)를 지원합니다. 회귀는 쉽게 말해, 결과값이 성별, 등급과 같은 몇 개의 클래스값이 아니라, 온도, 가격 등 다양한 값이 존재하는 문제를 말합니다.
회귀 트리 (Regression Tree)의 방법은 간단합니다. 분기 지표를 선택할 때 사용하는 index를 불순도 (Entropy, Gini index)가 아닌, 실제값과 예측값의 오차를 사용합니다.
수식을 보기 전, 간단한 예시를 먼저 살펴봅시다. tomaszgolan’s blog의 설명을 참고했습니다.
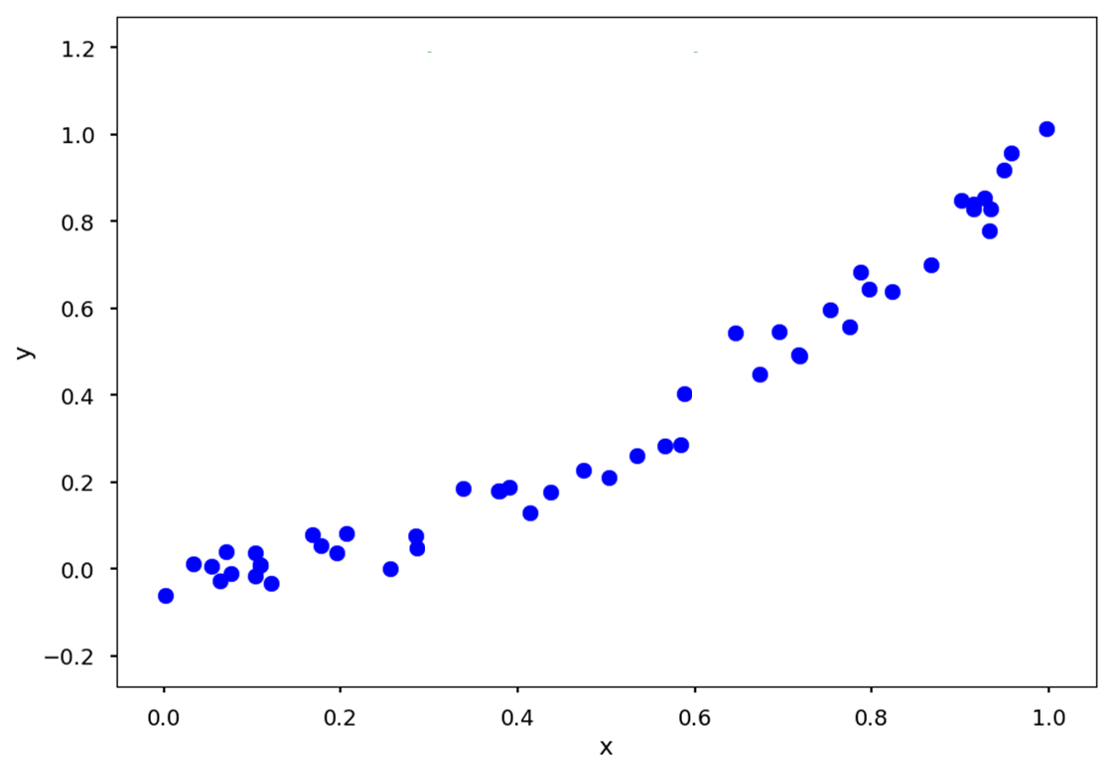
위와 같은 트렌드를 갖는 데이터를 기반으로, x에 따라 y를 예측하는 의사결정 나무를 만들고자 합니다.
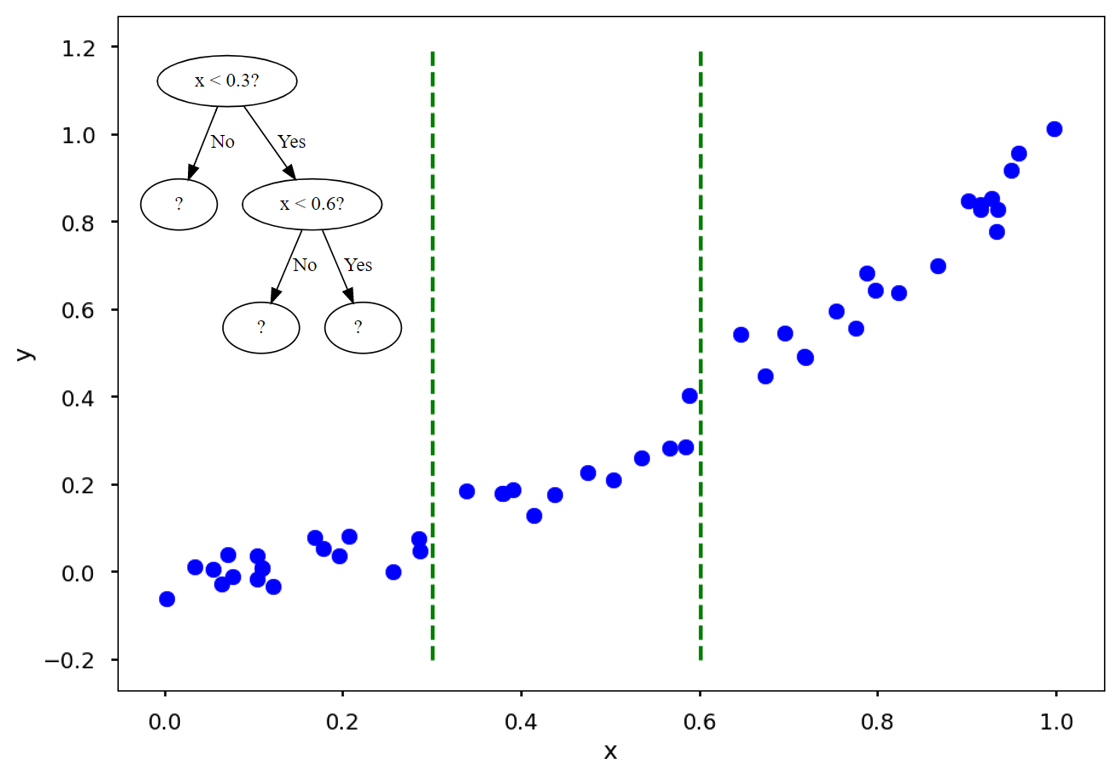
예를 들어 이렇게 \(x<0.3\)과 \(x<0.6\)을 지표로 하는 나무는 두 개의 초록 점선으로 데이터를 나눌 것입니다.
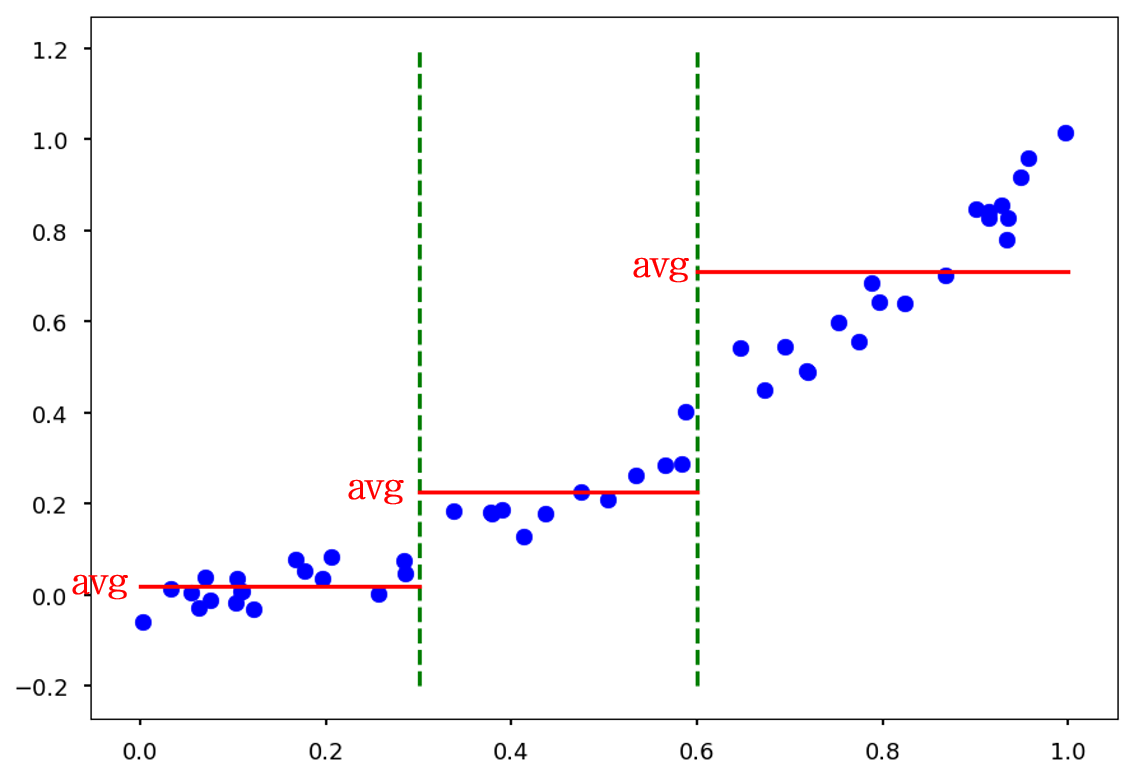
그리고는 각 구간의 x값이 들어올 경우, training data (파란 점)의 평균값 (빨간 실선)을 예측값으로 내놓습니다.
나무의 깊이가 깊어질 수록, 다시 말하면 데이터를 나누는 초록 점선이 촘촘하게 생길 수록 예측값과 실제값의 오차는 줄어들 것입니다.
이제 수식을 살펴봅시다.
실제값과 예측값의 오차는 \(RSS\)나 \(MSE\)와 같은 값으로 나타낼 수 있습니다.
\[ Residual\; Sum\; of\; Squares\; (RSS)=\sum_{j=1}^J \sum_{i \in R_j} (y_i - \hat{y}_{R_j})^2 \]
, where \(\hat{y}_{R_j}\) is the mean response for training observartions within \(j\)th box
아래 수식과 같이 Binary tree의 좌우가지에 대한 오차값 \(MSE{left}, MSE{right}\)을 계산하고, 좌우 가지에 해당하는 샘플 수의 비율 \(\frac{m{left}}{m}, \frac{m{right}}{m}(\)을 가중치로 곱해 전체 오차값 \(J(k, t_k)\)을 계산하여 지표간 비교를 통해 최적의 분기를 결정합니다.
\[ J(k, t_k)=\frac{m_{left}}{m}MSE_{left}+\frac{m_{right}}{m}MSE_{right} \]
Decision Tree의 단점: 과적합에 취약
ID3, C4.5, CART에 걸쳐 의사결정 나무 생성을 위한 알고리즘을 정리해보았습니다. 의사결정 나무 알고리즘은 간단하면서 효과적인 알고리즘이지만, 과적합 (Overfitting)에 취약하다는 단점이 존재합니다.
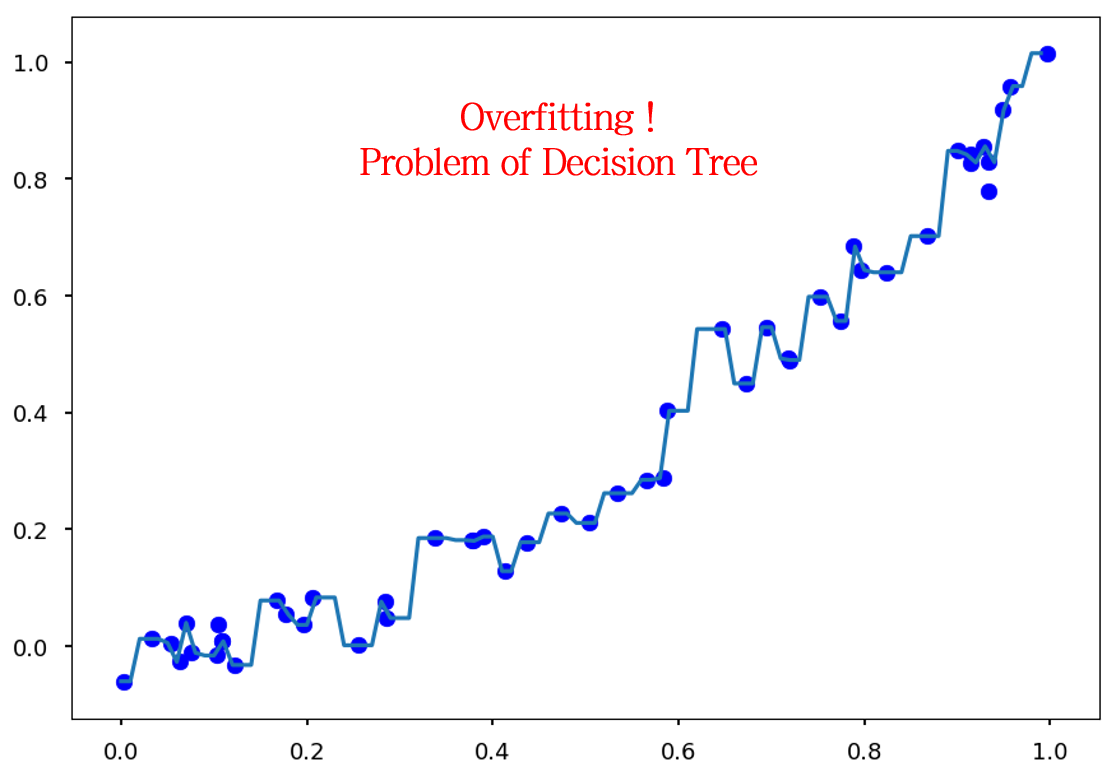
만약 Regression의 예시에서 모든 Training data가 개별 구간을 갖도록 의사결정 나무가 생성된다면 이 모델은 과적합된 모델이라고 할 수 있습니다. 즉, Training data에 너무 과도하게 학습된 모델입니다. 따라서 이러한 과적합을 막기 위해, 가지치기 (pruning) 과정을 수행합니다.
알고리즘에 따라 아래 예시와 같이 다양한 방법으로 사전 가지치기 (pre-pruning) 또는 사후 가지치기 (post-pruning)를 하기도 하지만, 단일 모델의 한계점은 여전히 존재합니다.
- 나무의 최대 깊이 (depth)를 제한
- 자식 노드의 최소 샘플 수를 설정
- impurity/error 의 최소값을 설정
- impurity/error 변화값의 최소값을 설정
이 문제를 해결하기 위해 사람들은 의사결정 나무를 여러개 만들어, 예측 결과를 종합하는 앙상블 (Ensemble) 알고리즘을 고안하였습니다.
다음 포스팅부터는 배깅 (Bagging), 부스팅 (Boosting), 스태킹 (Stacking) 등 다양한 앙상블 모델을 정리해고자 합니다.
다음 글 보기: 앙상블 (Ensemble)의 기본 개념

Leave a comment